YT 筆記：向量資料庫概念科普

在 RAG 架構中，ChatGPT 等 LLM 之所以能回答專屬領域問題，其關鍵在於已事先將相關文件、影像、資訊消化後存進資料庫並建立索引，當使用者詢問時，先透過索引找到資料，再由 LLM 彙整查詢結果給出答案。

來源

文字甚至影像之所以能被搜尋，是因為它先經 Embedding 轉為量並存進向量資料庫。文字轉為向量後，可跳脫單純的關鍵字比對，實現語意上比對，例如：查詢"狗"時，講到"Dog"的英文資料也能被篩選出來。而影像資料向量化後，則能實現用顏色、形狀以圖找圖的神奇效果。

在這套機制中，專為儲存及索引向量資料設計的向量資料庫是不可或缺的成員。向量資料庫的概念有點深奧，充斥 ANN、HNSW 之的神祕術語，不太好懂。YouTuber「Ele 實驗室」向來擅長用視覺呈現及淺顯比喻科普複雜資工理論(例如這部：YT 筆記 - 資安科普：為什麼 MD5 不再安全？，大推)，最近發現這部：

【上集】向量数据库技术鉴赏

再次把向量資料庫原理解釋到國中生都能懂，是很好的科普教材，搞懂餘弦相似性、KNN、ANN、量化、PQ、HNSW 等專業術語是深入 RAG 開發的基礎，故循例筆記備忘兼分享。

1. 為什麼要用高維度向量表示資料？
   想像一下，如果我們要區分數以百種的狗，最簡單的方法用體型、長短毛、毛色、嘴巴長度... 等特徵區別，每一個特徵可想成一個維度，維度愈高，愈能精細區別不同項目。此一概念可轉化為多維量向量，特徵變為一串數字後，後續便可進行數學運算，用演算法完成我們想要的任務。
   將高維空間映對成 2D 平面方便說明，我們可觀察到一些有趣特性：
   1. 性質相近者會群聚
      
   2. 向量關係可以用來類推二者關係，例如：貓到老鼠的線與警察到小偷的線呈現平行
      
   3. 兩段語意相近的文字轉換成的向量數據也會有相似性，從而讓我們找出相關的文字
2. 為什麼需要向量資料庫？
   基於資料特性差異，傳統資料庫不適合儲存向量資料，改用向量資料庫更能滿足效能及效率要求。
3. 如何比對向量資料？
   向量資料是透過比較相似性找尋相關內容，主要靠最鄰近搜索（Nearest Neighbor Search, NNS）演算法。無腦做法是將查詢對象的向量跟所有資料的向量全部比對一次，用餘弦相似性(https://zh.wikipedia.org/zh-tw/%E4%BD%99%E5%BC%A6%E7%9B%B8%E4%BC%BC%E6%80%A7)或歐幾里得距離找出最近者，此法雖精準但耗時無效率。
   一個改良思維是先縮小範圍，例如用 K-Means (k-平均演算法，K-Nearest Neighbors/KNN)將點分類，每次只查找所屬類別的點：
   
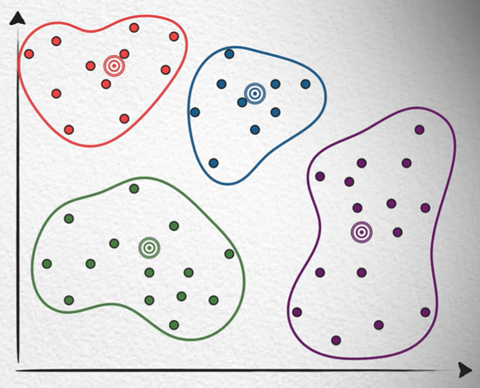
   只找所屬分類極有可能出現「最近的點隸屬另一分類」的狀況，此問題可透過增加分類數量，及連帶搜索相近分類改善，雖能提升精準度卻勢必拖慢速度。
   另一種做法是 Locality Sensitive Hashing (位置敏感雜湊法)，使用位置愈近碰撞機率愈高的雜湊演算法，將相近的點集合在一起放入同一個 Bucket。實踐方式是用隨機線或隨機超平面將所有點劃分為 0 或 1，每條線/每個平面決定一個位元組成一串編碼，則位置愈近的點編碼相同的位數愈多，再用分段比對提高找到相近點的機率。
   以上方法都必須在品質與速度間取捨，沒有絕對精準的解法，故這些演算法也被稱為 Approximate Nearest Neighbors (ANN) 近似最鄰近搜索。
4. 向量資料庫如何減少記憶體耗用量？
   高維度向量資料佔用記憶體空間十分驚人。以 128 維資料為例，浮點數 FP32 = 4 Bytes，一個向量需要 512 Bytes，一千萬筆就會佔用 4.77GB，而實務的維度常大於 128 維，資料遠超過一千萬筆，耗用空間可觀。一個有效減量做法是 Product Quantization 乘積量化，例如以 K-Means 質心座標當成該群所有點的座標(類似有損壓縮)：
   
   如此只需記錄質心向量值給編碼值，並用對照表保存質心向量。實務上高維度需切割的聚落數及質心數將爆炸成長(例如：2⁶⁴)，記錄質心向量所需空間遠大於量化節省空間，得不償失，稱之「維度災難」。解法是將高維向量分割成多個低維子向量，在子向量進行 K-Mean 訓練及量化。例如：把 128 維分割成 8 個 16 維子向量空間，子向量只需 256 個聚落，將八個子空間編碼值合在一起表示 128 維的點(Cartesian Product 笛卡爾積)，這個做法稱為 Product Quantization (積量化，PQ)。如此可將資料量由 4.77GB 降到 76 MB。
5. 主流向量資料庫常採用什麼方法加快搜索？
   使用者對速度與查詢品質敏感，用記憶體換取二者提升很值得。基於圖論的 Hierachical Navigable Small World (HNSW) 即是一例。
   直覺做法是用德勞內三角剖分法(Delaunay Triangulation Algorithm)建立所有點的圖結構，但此法有路徑效率不佳的問題。NSW 改良做法是將點一一放回去時跟最近的三個點建立連線，之後將線區分為長連結跟短連結，先用長連結快速度跳到目標附近，再走短連結到達目的節點。(先粗快，後細慢)
   改良版 HNSW 將路徑分層，確保可以穩定先長路徑再短路徑走到目的，雖然會多耗用記憶體記錄多層路徑，卻能有效提升搜尋速度及品質。
   
   現代向量資料量會綜合上述各種演算法達成最佳效果。