PowerShell 小工具 - 簡易檔案編碼識別

我有個小需求是要檢查專案程式檔是否混雜 Unicode、BIG5 等非 UTF-8 編碼，類似任務過去用 C# 寫過，例如：BIG5 GB2312繁簡編碼快篩、潛盾機－解決VS2015程式檔BIG5相容問題，為了方便在工作上應用，我想寫個 PowerShell 版，以上是本次的企劃。

由於只需識別 UTF-8、Unicode、BIG5 三種編碼，且輸出結果是作為檢核警示，後續會有人工確認，不需要花太多時間涵蓋各種語系，邏輯也不需要 100% 精準，算是一次簡單任務。我的構想是用 File.ReadAllBytes() 讀入檔案 byte[] 後分別用 Encoding.UTF8、Encoding.Unicode 的 GetString() 轉成字串，檢測其中是否出現轉碼失敗的 � 字元來推測。

BIG5 的部分比較麻煩，如 GB2312 簡體中文或 Shift JIS 日文等泛 ANSI 類編碼，用 Encoding.GetEncoding(950) 轉字串，大部分字元可以對映到有效的繁體字碼區，但非中文常用字，無法對映的無效字元會變成 ?。我慣用的解法是用「無效字元*3 + 次常用字) / 總字元數」計算 BadSmell 指數，猜測它不是 BIG5 的機率。

程式範例如下：

function IsBig5([byte[]]$data) {
    $symbol = 0
    $common = 0
    $rare = 0
    $unknow = 0
    $ascii = 0
    $isDblBytes = $false
    $dblByteHi = 0
    foreach ($b in $data) {
        if ($isDblBytes) {
            if (($b -ge 0x40 -and $b -le 0x7e) -or ($b -ge 0xa1 -and $b -le 0xfe)) {
                $c = $dblByteHi * 0x100 + $b
                if ($c -ge 0xa140 -and $c -le 0xa3bf) {
                    $symbol++
                }
                elseif ($c -ge 0xa440 -and $c -le 0xc67e) {
                    $common++
                }
                elseif ($c -ge 0xc940 -and $c -le 0xf9d5) {
                    $rare++
                }
                else {
                    $unknow++
                }
            }
            else {
                $unknow++
            }
            $isDblBytes = $false
        }
        elseif ($b -ge 0x80 -and $b -le 0xfe) {
            $isDblBytes = $true
            $dblByteHi = $b
        }
        elseif ($b -lt 0x80) {
            $ascii++
        }
    }
    $total = $ascii + $symbol + $common + $rare + $unknow
    $badSmell = [float]($rare + $unknow * 3) / $total
    return $badSmell -lt 0.1;
}
function RoughDetectEncoding {
    param(
        [Parameter(Mandatory = $true)][string]$fileName
    )
    $res = @{
        Encoding = 'unknown'
        Content = ''
    };
    $bytes = [System.IO.File]::ReadAllBytes($fileName)
    $res.Content = [BitConverter]::ToString($bytes)
    $big5Enc = [System.Text.Encoding]::GetEncoding(950)
    # 若不容許 BIG5 夾雜無效編碼字元，
    # 可改條件為 $big5Enc.GetBytes($big5Enc.GetString($bytes)).Length -eq $bytes.Length -and (IsBig5 $bytes)
    if (IsBig5 $bytes) {
        $res.Encoding = 'big5'
        $res.Content = $big5Test
        return $res
    }   
    $utf8Test = [System.Text.Encoding]::UTF8.GetString($bytes)
    if (!$utf8Test.Contains("�")) {
        $res.Encoding = 'utf-8'
        $res.Content = $utf8Test
        return $res
    }
    $unicodeTest = [System.Text.Encoding]::Unicode.GetString($bytes)
    if (!$unicodeTest.Contains("�")) {
        $res.Encoding = 'unicode'
        $res.Content = $unicodeTest
        return $res
    }
    return $res
}

@('utf8.txt', 'unicode.txt', 'big5.txt', 'gb2312.txt', 'jis.txt') | ForEach-Object {
    $fileName = $_
    $res = RoughDetectEncoding -fileName $fileName
    Write-Host "File: $fileName, Encoding: $($res.Encoding)" -ForegroundColor Cyan
    Write-Host "$($res.Content)" -ForegroundColor White
}

我弄了簡單測試，同一段文字分別用 UTF-8、Unicode、BIG5 儲存，再加上簡體中文跟日文：

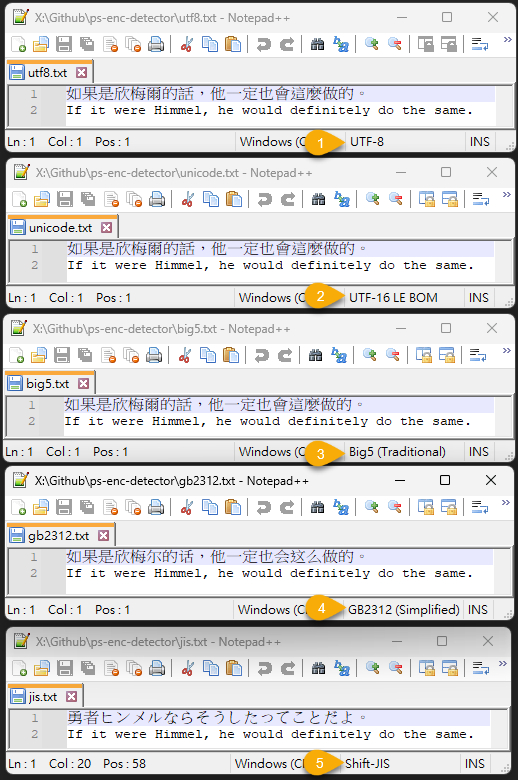
測試成功：

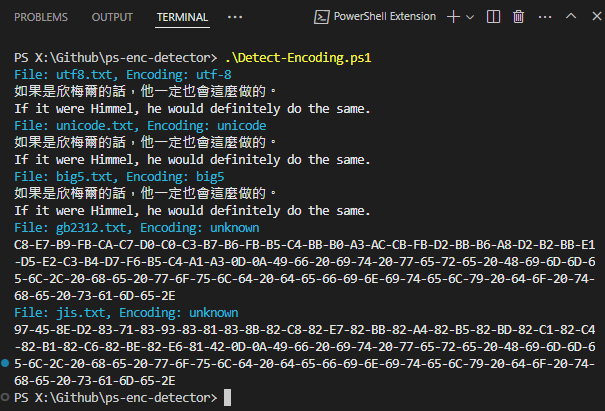
This article provide a rough but simple to to detect the encoding of text file with PowerShell.