Coding4Fun - 也來偷東西(誤)之背包問題 .NET 式解法
| | | 4 | |
前幾天我玩了八皇后(喂),部落格跟 FB 都有朋友提到另一個演算法經典問題 - 背包問題。
簡單來說,背包問題是假設你有一個背包跟數件重量與價值不一的物品,在不超過背包負重上限的前題下,要決定該放入哪些物品使其總價值最大化。經典案例是小偷闖空門,面對一屋子值錢家當,我們要幫他想背包裝進哪些東西賺最多。(雖說是背包,但只是抽象的重量上限概念,全無體積考量,我還看到有題目要在背包裡放進電冰箱的,花惹發!)
背包問題還有一些變形:
- 0/1 背包問題 - 每種物品只有一個,只有放入跟不放入的選擇。(就是小偷入屋行竊案例,拿與不拿的抉擇)
- 無界(Unbounded)背包問題 - 每種物品有無限多個,可以放入一個或多個
- 有界(Bounded)背包問題 - 每種物品可以放入一個或多個,但各物品有其數量上限
- 湊金額問題(Money Changing) - 放入物品要剛好湊到指定金額
- 找錢問題(Change Making) - 給紙鈔找零錢,硬幣數量愈少愈好
- 派系投票問題(Partition Problem) - 投票者由派系組成,每個派系成員立場一致,研究派系影響力
這篇我只挑較常見的 0/1 背包問題跟無界背包問題來解。跟上回一樣,網路上比短比快比小的程式範例多不勝數,我的版本特色會是使用 C# 並走 .NET 風格,大量使用 IEnumerable<T>、LINQ 跟物件導向概念,力求直覺化好理解。
開始前先定義物件(Item)與問題(Problem)兩個類別:
public class Item
{
public string Name { get; set; }
public int Weight { get; set; }
public int Value { get; set; }
public Item(string name, int weight, int value)
{
Name = name;
Weight = weight;
Value = value;
}
public override string ToString()
{
return $"{Name} (W:{Weight} / V:${Value})";
}
}
public class Problem
{
public Item[] Items;
public int MaxWeight;
public bool Duplicatable;
public Problem(int maxWeight, bool allowPural, IEnumerable<Item> items)
{
Items = items.ToArray();
Duplicatable = allowPural;
MaxWeight = maxWeight;
}
}
簡單背包問題可以靠暴力破解,但是當物品種類一多會算到地老天荒! 故標準解法是用動態規劃(Dynamic Planning),畫出不同重量單位的格子(例如:8 公斤背包分成 1 公斤, 2 公斤, ... 到 8 公斤 8 個格子),接著每項物品輪流對這個 8 個格子(8 種不同重量的情況)做決策,看放進去價值較高,還是改放其他物品較划算。有一種狀況是放入該物品後背包重量還有剩,則剩下重量可以再放入其他物品,此時先前算過 1, 2, 3 公斤的小重量的結果即派上用場了,直接取值求解。實際的演算過程有點複雜,可能得把格子晝出來才好理解,網路有一些解說範例(稍後會提到),在此不花篇幅細說。
由於我同時想試暴力破解跟動態規劃,故我先定義一個計算器的基底類別,把兩種演算法共用的邏輯放進來:
using System;
using System.Collections.Generic;
using System.Diagnostics;
using System.Linq;
using System.Text;
namespace Knapsack
{
/// <summary>
/// 背包問題計算機基底類別
/// </summary>
public abstract class CalculatorBase
{
public int MaxWeight; //背包最大負重
public Item[] Items; //可放入物品清單
public bool Duplicatable; //物品是否可重複
protected abstract string AlgorithmName { get; } //演算法名稱
protected class Answer //計算結果
{
public IEnumerable<Item> Items; //背包內物品清單
public int MaxValue => Items.Sum(o => o.Value); //最高價值
public int ExecCount; //運算次數
}
public CalculatorBase(Problem problem)
{
MaxWeight = problem.MaxWeight;
Items = problem.Items;
Duplicatable = problem.Duplicatable;
}
protected abstract Answer Calculate(); //抽象方法,實作演算邏輯
public void Run(bool warmup = false)
{
var sw = new Stopwatch();
sw.Start();
var answer = Calculate();
sw.Stop();
Console.ForegroundColor = warmup ? ConsoleColor.DarkGray : ConsoleColor.Yellow;
Console.WriteLine($"====== {this.AlgorithmName} ======");
if (!warmup) Console.ResetColor();
Console.WriteLine($"最高價值:{answer.MaxValue}");
Console.WriteLine($"物品清單:{string.Join(" / ", answer.Items.Select(o => o.ToString()).ToArray())}");
var dura = sw.ElapsedMilliseconds > 1 ?
$"{sw.ElapsedMilliseconds:n0} ms" : $"{sw.ElapsedTicks:n0} ticks";
Console.WriteLine($"執行時間:{dura} ( {answer.ExecCount:n0} 次 )");
}
}
}
Duplicatable 屬性用來決定背包內的物品是否允許重複出現,設為 false 時為 0/1 背包問題,設為 true 則為無界背包問題。
先來看暴力破解法,BruteForceCalculator 繼承 CalculatorBase,宣告一個背包類別,用 Explore() 跑遞迴,找出不會讓目前背包超重的物品項目一一放入,放入後再依剩餘重量再找出不超重的物品項目一一放入,不斷輪迴直到放不下為止,過程中找出價值最高的組合:
public class BruteForceCalculator : CalculatorBase
{
public BruteForceCalculator(Problem problem) : base(problem) { }
protected override string AlgorithmName => "暴力破解法";
public class Knapsack //模擬背包行為
{
public List<Item> Items = new List<Item>();
public int CurrentValue = 0;
public int AllowedWeight = 0;
public Knapsack(int maxWeight)
{
AllowedWeight = maxWeight;
}
public void AddItem(Item item) //放入物品
{
Items.Add(item);
CurrentValue += item.Value;
AllowedWeight -= item.Weight;
}
public void RemoveItem(Item item) //取出物品
{
Items.Remove(item);
CurrentValue -= item.Value;
AllowedWeight += item.Weight;
}
}
protected override Answer Calculate()
{
Knapsack bag = new Knapsack(MaxWeight);
MaxValueItems = bag.Items.ToArray();
Explore(bag, Items.ToList());
return new Answer
{
Items = MaxValueItems,
ExecCount = CallCount
};
}
public Item[] MaxValueItems = null;
public int MaxValue = 0;
int CallCount = 0;
public void Explore(Knapsack knapsack, List<Item> options)
{
//篩選小於背包剩餘可負重的物品一一嘗試
//這裡直接用Where過濾,若要提高效能需再優化
foreach (var item in options.Where(o => o.Weight <= knapsack.AllowedWeight))
{
CallCount++;
knapsack.AddItem(item); //放入物品
if (knapsack.CurrentValue > MaxValue) //若超越最高記錄就記錄
{
MaxValueItems = knapsack.Items.ToArray();
MaxValue = knapsack.CurrentValue;
}
if (!Duplicatable) //若不允許物品重複,已放入背包的項目需移出選項
Explore(knapsack, options.Except(new Item[] { item }).ToList());
else
Explore(knapsack, options.ToList());
knapsack.RemoveItem(item);
}
}
}
再來是動態規劃法:
public class DynamicPlanningCalculator : CalculatorBase
{
public DynamicPlanningCalculator(Problem problem) : base(problem) { }
protected override string AlgorithmName => "動態規劃法";
public class Cell
{
public List<Item> Items { get; set; }
public int TotalValue { get; set; }
public int TotalWeight { get; set; }
//傳入物品集合建立格子
public Cell(IEnumerable<Item> items)
{
Items = items.ToList();
TotalValue = items.Sum(o => o.Value);
TotalWeight = items.Sum(o => o.Weight);
}
public Cell() : this(new List<Item>()) { } //空格子
//其他格子的內容再加上指定物品
public Cell(Cell cell, Item item) : this(cell.Items.Concat(new Item[] { item })) { }
//在格子放在指定物品
public Cell(Item item) : this(new Item[] { item }) { }
}
protected Cell[,] Cells = null;
protected override Answer Calculate()
{
var items = Items;
var rowCount = items.Length;
var colCount = MaxWeight;
Cells = new Cell[rowCount, colCount];
for (var row = 0; row < rowCount; row++)
{
var item = items[row]; //每一列處理一種物品
for (var col = 0; col < colCount; col++)
{
var cellMaxWeight = col + 1; //本欄的最大重量單位
//正上方的格子,若為第一列則為空格
var upperCell = row > 0 ? Cells[row - 1, col] : new Cell();
Cell currCell;
//物品超重放不進去,直接取上方格子或空格子
if (item.Weight > cellMaxWeight)
currCell = upperCell;
else //背包放得下
{
//先放入物品本身,如果有其他更划算的再換掉
currCell = new Cell(item);
//剩餘重量還可用來裝值錢東西
var weightLeft = cellMaxWeight - item.Weight;
if (weightLeft > 0) //若背包負重還有剩
{
if (Duplicatable)
//允許物品重複,由同列取剩餘重量最大價值組合加上本物品
currCell = new Cell(Cells[row, weightLeft - 1], item);
else if (row > 0)
//每個物品只能有一個,從上一列取得剩餘負重最大價值組合加上本物品
currCell = new Cell(Cells[row - 1, weightLeft - 1], item);
}
//若搞了半天沒上一列值錢,取上一列
if (currCell.TotalValue < upperCell.TotalValue)
currCell = upperCell;
}
Cells[row, col] = currCell;
}
}
return new Answer
{
Items = Cells[rowCount - 1, colCount - 1].Items, //最右下角為最高價值
ExecCount = rowCount * colCount
};
}
}
我讓格子(Cell)成為物件,Cell 類別運用了建構式多載(Overloading),提供四種建立方式:傳入物品集合、空格子、傳入另一個格子跟新放入物品、放入單一物品,建構式可使用 this(...) 引用其他建構式簡化程式。計算比對原理我有寫註解,希望說明得夠清楚。
程式寫完來實測一下。我找了網路上的範例,有題目有答案才知自己有沒有算錯。
測試一
.NET 程式第一次執行因涉及靜態成員執行、JIT 編譯等因素、速度偏慢(延伸閱讀:.NET 首次執行偏慢現象之 JIT 編譯效應觀察),故測試會跑三次,第一次為暖身不計。
第一題來自這篇 Knapsack Problem, Dynamic programming, 0/1 背包問題 引用的農場文章,例子單純且圖解步驟詳細,是目前我看到好理解的說明。花了點時間才找到原出處,應該來自算法图解這本書。
static void Main(string[] args)
{
Test1();
Console.ReadLine();
}
static void Test(Problem problem)
{
Console.ForegroundColor = ConsoleColor.Cyan;
Console.WriteLine(
$"【問題】重量上限 = {problem.MaxWeight} / 物品種類 = {problem.Items.Length} / 允許物品重複 = {(problem.Duplicatable ? "是" : "否")}");
Console.ResetColor();
for (var i = 0; i < 3; i++)
{
var bfc = new BruteForceCalculator(problem);
bfc.Run(i == 0); //i==0 為暖身
var dpc = new DynamicPlanningCalculator(problem);
dpc.Run(i == 0); //i==0 為暖身
}
Console.WriteLine();
}
static void Test1()
{
var problem = new Problem(4, false, new Item[]
{
new Item("吉他", 1, 1500),
new Item("音響", 4, 3000),
new Item("筆電", 3, 2000)
});
Test(problem);
}
執行結果,兩種算法結果相同速度差不多,問題太簡單,暴力破解計算次數反而還比較少。

測試二
題目來自良葛格的演算法文章,每種水果可以放一個或多個,為無界背包問題:
static void Test2()
{
//REF: https://openhome.cc/Gossip/AlgorithmGossip/KnapsackProblem.htm
var problem = new Problem(8, true, new Item[]
{
new Item("李子", 4, 4500),
new Item("蘋果", 5, 5700),
new Item("橘子", 2, 2250),
new Item("草莓", 1, 1100),
new Item("甜瓜", 6, 6700)
});
Test(problem);
}
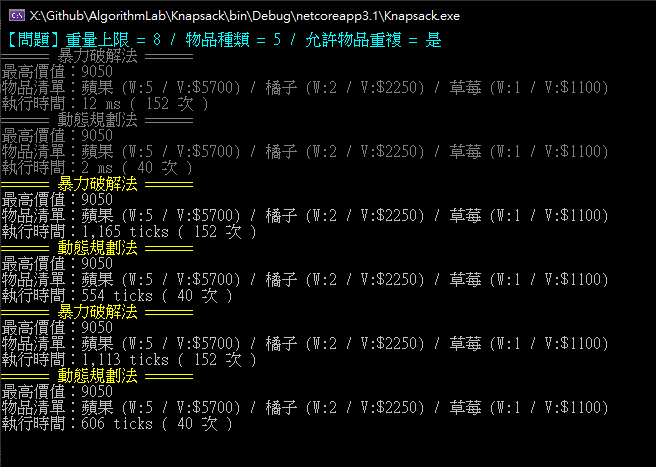
對答案,9050,正解! 而這個案例有顯現動態規劃的優勢,只需要算 5*8 = 40 次,而暴力破解要算 152 次,時間多一倍。
測試三
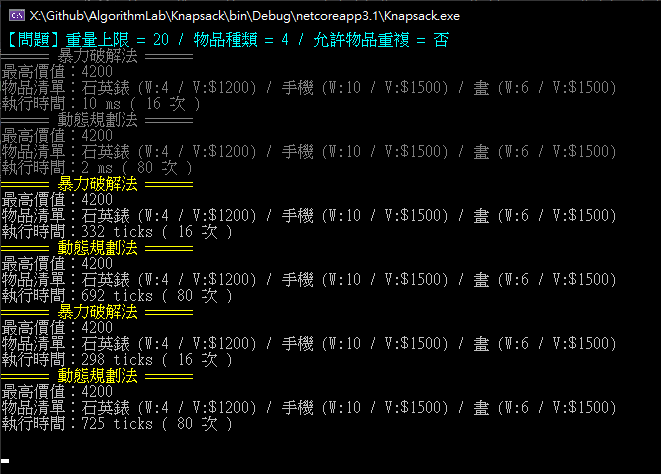
這個題目來自用動態規劃解決問題:零壹背包問題(0/1 Knapsack Problem),特別處在於背包上限 1000 克,物品重量為 200、500、300、850 克,動態規劃時要依不同重量逐一畫格子,但沒必要以 1 克為單位搞出 1000 格,我是取每 50 克一個單位。
static void Test3()
{
//REF: https://magiclen.org/dynamic-programming-0-1-knapsack-problem/
var wu = 50;
var problem = new Problem(1000 / wu, false, new Item[] {
new Item("石英錶", 200/wu, 1200),
new Item("手機", 500/wu, 1500),
new Item("畫", 300/wu, 1500),
new Item("平板電腦", 850/wu, 4000),
});
Test(problem);
}
測試四
目前為止的測試還不太感受得到動態規劃的威力,反正暴力破解也辦得到,速度差不多有時計算次數還更少。這把玩大一點的,把物品種類提高到 20 種看看會怎樣?
static void Test4()
{
var rnd = new Random();
var randomItems = Enumerable.Range(1, 20)
.Select(o => new Item("物品", rnd.Next(100) + 1, rnd.Next(400) * 10 + 10))
.ToArray();
var problem = new Problem(randomItems.Sum(o => o.Weight) / 4, false, randomItems);
Test(problem);
}
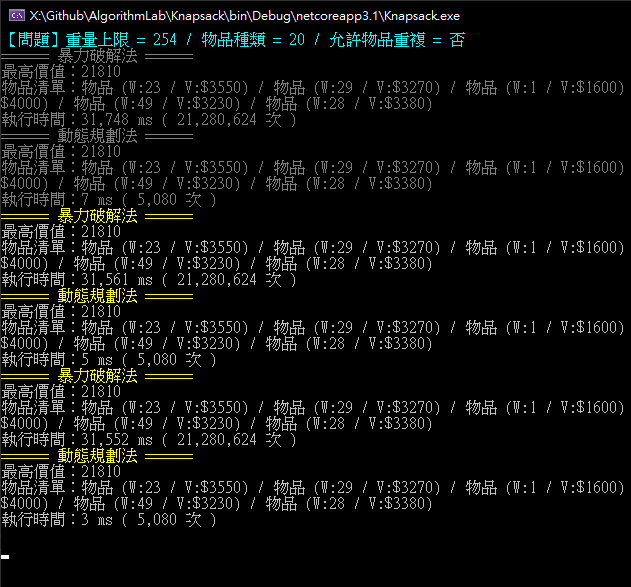
薑! 薑! 薑! 薑~~~ 31 秒對上 0.005 秒,2,128 萬次對上 5,080 次,知道為什麼背包問題要用動態規劃來解了吧!
【2020-10-30 更新】範例程式碼已上傳至 Github。
This article shows how to use C# to write bructe-force and dyanamic planning algorithm to solve Knapsack Problem.
Comments
# by Laurence
算法圖解這本的原書有出繁中翻譯版 https://www.kingstone.com.tw/basic/2013180003950/#&gid=1&pid=17
# by chming
to Jeffrey 黑大你好,關於背包問題我有個愚蠢的問題想問 1.背包問題跟聯立不等式是不是類似的情境? 還是跟排列組合類似? 若是的話,是不是用紙筆得出最佳解可能會比寫程式還快? 2.延伸問題想問說這種組合最佳化的問題, 要列出組合排名榜(ex:前5名最佳組合) 是不是只能讓程式窮舉法(暴力破解) 先將組合得出的價值用個矩陣暫存起來 再用某種排序演算法得出前5名? 最後請問你這篇實作的程式能否開放在你個人github嗎? P.S. https://bestdori.com/tool/teambuilder/ 我個人目前很想仿造這網站的隊伍模擬器功能,想套用在其它遊戲上 感覺這功能跟背包問題、一筆畫問題都屬於組合最佳化的課題 無奈我實力和邏輯欠佳,但我真的覺得這情境如果能搞懂的話 我會對此很高興且追求性價比感覺能應用在很多情況
# by Jeffrey
to chming, 1. 用紙筆算會不會更好? 關鍵在計算量! 當題目簡單,與其花時間寫成程式不如用紙筆算一下就出來。但若問題複雜到電腦要算上十分鐘,用紙筆恐怕得用掉兩箱 A3 紙加三打原子筆跟七天時間(如果最後人沒瘋掉的話)。另一個角度是,若某個電腦需要算十分鐘的問題存在一張 A4 紙可以搞定的紙筆解法,那是程式沒採用最有效率解法,應該改寫優化。電腦擅長精大量反覆計算,人腦負責想出計算原理,把枯燥的計算工作交給電腦執行,二者是互補的。而以背包問題為例,文章最後的例子用動態規劃得計算超過 5000 次,這種計算量用電腦會比用紙筆更符合效率。 2. 不管暴力破解或用動態規劃,將只取最大值的邏輯稍加修改成最前 N 名,便能改成取前 5 名最佳組合,宣告一個長度為 5 的陣列用來保存前 5 名的資料,過程中發現其值比第 5 名高,就依其值高底插到 5 至 1 名前方,把目前的第 5 名刷掉,迴圈或遞迴跑完,前 5 名就出爐了。 程式碼我放上 Github 了,連結已更新於本文。
# by Python路過吾好錯過
def knapsack(weights, prices, capacity): n = len(weights) dp = [[0 for _ in range(capacity + 1)] for _ in range(n + 1)] for i in range(1, n + 1): for w in range(1, capacity + 1): if weights[i - 1] <= w: dp[i][w] = max(dp[i - 1][w], dp[i - 1][w - weights[i - 1]] + prices[i - 1]) else: dp[i][w] = dp[i - 1][w] return dp[n][capacity] def knapsack_1D(weights, prices, capacity): n = len(weights) dp = [0] * (capacity + 1) for i in range(1, n + 1): for w in range(capacity, weights[i - 1] - 1, -1): dp[w] = max(dp[w], dp[w - weights[i - 1]] + prices[i - 1]) return dp[capacity]