Coding4Fun - 八皇后問題之 .NET 式解法
 |  | 3 |  |  |
前幾天學到一個新名詞 - 八皇后問題,傳說是所有資工系學生都玩過的演算法經典案例。非本科系沒學過演算法,但自覺遞迴難不倒我,便想試試在不看範例的前題下自己能否用 C# 土砲出答案(沒在學生時代被爆雷的人才有的玩法 XD),列出傳說中的 92 組解?
天資不足,卡在座標換算公式很久,只能笨笨地在紙上畫格子推算對應值,搞了好久,總算趕在午夜鐘響電腦變南瓜前夕解出來:

這個經典問題在網路上可找找到數不清的範例,維基百科直接附了 C、Pascal、Java 版範例,良葛格更是一口氣寫完 Toy、C、Java、Python、Scala、Ruby、JavaScript、Haskell、Prolog 九種版本,其程式碼之簡潔令人咋舌。這題目如要鑽研方向很多,可以求快、求精簡、求記憶體用量小... 要比這些我的版本應該都上不了檯面,不過,好像沒人像我一樣用 HashSet、LINQ 來解,就分享一下這個新奇又有趣的寫法吧!
把昨天的程式整理一下,我寫了一個以 HashSet<int> 儲存可用空格、List<int> 記錄皇后位置,大量用 LINQ 方法,並採物件導向的版本,含註解不超過 100 行:(註:HashSet<int> 用 List<int> 取代其實也可行,但因需反覆比對特定值是否存在,其查找效率為 O(1) 速度較快,參考:[小抄]選擇合適的 .NET 集合類型 by Huan-Lin 學習筆記)
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
namespace LinqEightQueens
{
public class Chessboard
{
const int GRID_SIZE = 8;
const int DIG_SHIFT = 10;
const int QUOTA = 8;
/// <summary>
/// 棋盤空格
/// </summary>
public HashSet<int> Slots { get; set; }
/// <summary>
/// 皇后位置
/// </summary>
public List<int> QueenPositions { get; set; }
/// <summary>
/// 空白棋盤
/// </summary>
public Chessboard()
{
//產生 11,12,...,18,21,22...28,...88 格子座標陣列
Slots = new HashSet<int>(
Enumerable.Range(1, GRID_SIZE)
.SelectMany(x => Enumerable.Range(1, GRID_SIZE)
.Select(y => x * DIG_SHIFT + y))
);
QueenPositions = new List<int>();
}
/// <summary>
/// 現有棋盤在特定位置放上皇后生出新棋盤
/// </summary>
/// <param name="board">現有棋盤</param>
/// <param name="pos">皇后位置</param>
public Chessboard(Chessboard board, int pos)
{
Slots = new HashSet<int>(board.Slots.Except(new int[] { pos }));
QueenPositions = new List<int>(board.QueenPositions.Concat(new int[] { pos }));
var qX = pos / DIG_SHIFT;
var qY = pos % DIG_SHIFT;
Action<int, int> removeSlot = (px, py) =>
{
//超出範圍時忽略
if (px < 1 || px > GRID_SIZE || py < 1 || py > GRID_SIZE) return;
var v = px * DIG_SHIFT + py;
if (Slots.Contains(v)) Slots.Remove(v);
};
for (var x = 1; x <= GRID_SIZE; x++)
{
for (var y = 1; y <= GRID_SIZE; y++)
{
removeSlot(x, qY); //水平線
removeSlot(qX, y); //垂直線
}
var tx = x + (qX - qY);
removeSlot(tx, x); //左上右下斜線
tx = qX + qY - x;
removeSlot(tx, x); //右上左下斜線
}
}
/// <summary>
/// 空格數小於未放皇后數量,無解
/// </summary>
public bool NoSolution => Slots.Count < QUOTA - QueenPositions.Count;
/// <summary>
/// 皇后數量達標
/// </summary>
public bool TouchDown => QUOTA == QueenPositions.Count;
//印出棋盤
public void Print()
{
for (var y = 1; y <= GRID_SIZE; y++)
{
for (var x = 1; x <= GRID_SIZE; x++)
{
var pos = x * DIG_SHIFT + y;
if (QueenPositions.Contains(pos))
{
Console.ForegroundColor = ConsoleColor.Red;
}
else
{
Console.ForegroundColor =
Slots.Contains(pos) ? ConsoleColor.White : ConsoleColor.Yellow;
}
Console.Write("█ ");
}
Console.WriteLine();
}
Console.ResetColor();
}
}
}
Chessboard 物件有個有趣功能,可在任意位子放上皇后看它的米字線,我用它來驗算座標公式有沒有寫錯:
var board = new Chessboard();
var poses = new int[] { 11, 24, 33, 27, 65 };
foreach (var pos in poses)
{
Console.WriteLine($"== Position {pos} ==");
new Chessboard(board, pos).Print();
}

至於求解的演算法還挺直覺的,每放下一枚皇后,就將其米字線覆蓋的格子從 Slots 移除,餘下的即為還能放皇后的位置,用遞迴試著在餘下格子逐一放上皇后,遇到剩餘格子數過少(不足以容納剩下皇后數)便放棄探索,探索一路深入到放滿八個為止。(註:好像這就是所謂的回溯演算法 Backtracking Algorithm)
複雜邏輯都寫在 Chessboard,主程式的遞迴相對簡單。一開始產生一個全空的棋盤,在各一座標放上皇后產生一個新棋盤,檢查新棋盤還放不放得下剩餘的皇后,若還有機會就繼續對它展開探索,不斷深入,直到放滿八個把結果印出來。
class Program
{
static void Main(string[] args)
{
var board = new Chessboard();
Explore(board);
Console.ReadLine();
}
static int resIdx = 1;
static void Explore(Chessboard board)
{
//放皇后的順序一律由左上到右下,排除重複組合
var minPos = board.QueenPositions.Any() ? board.QueenPositions.Max() : 0;
foreach (var pos in board.Slots.Where(o => o > minPos))
{
var newBoard = new Chessboard(board, pos);
if (newBoard.TouchDown)
{
Console.WriteLine($"=== Result {resIdx++:00} ===");
newBoard.Print();
}
else if (!newBoard.NoSolution)
{
Explore(newBoard);
}
}
}
}
測試成功!
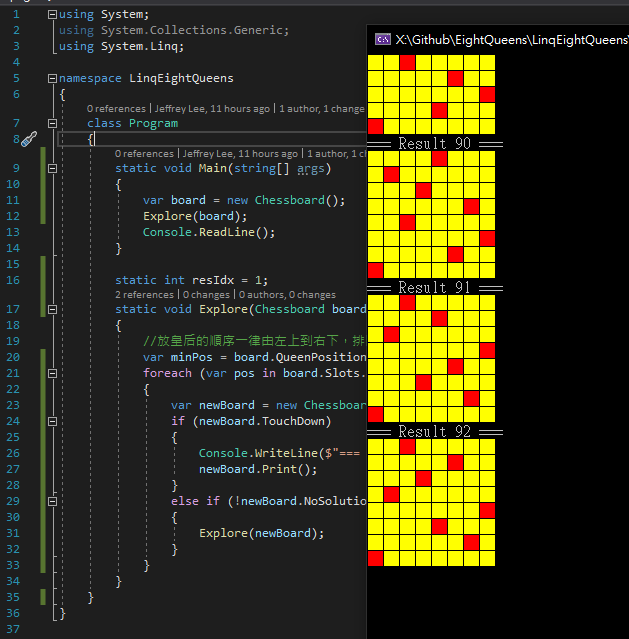
【後記】有時我在想:自己這麼熱愛 Coding,如果當年唸的是資工或資管會不會更精彩?後來想想也未必,主動挑自己有興趣的東西學習是一回事,被逼著啃完生硬理論,管它苦的酸的都要吞好吞滿又是另一回事,搞不好我會在被離散數學、資料結構、演算法的摧殘下,早早做出自己不適合走這行的結論,哈!
【2020-10-30 更新】範例程式碼已上傳至 Github。
Solving Eight Queen puzzle with HashSet and LINQ.
Comments
# by Huang
推後記這段,可參考:資工必修科目
# by Huang
可以繼續再解:背包問題
# by ByTIM
資管的路過,大學(四年前)就寫寫小程式,沒解到八皇后,程式基礎都靠高中學到的。 有時在想我這能力,竟然可以吃程式碼的工作,會不會對不起老闆。