1

我對非對稱式加密及數位簽章的理解主要仍靠十幾年前自學的一點皮毛，時光飛逝，隨著密碼學發展跟因應日益強大的電腦破解算力考量，現在常用的公私鑰演算法跟我想像的已有很大出入。前陣子在弄 Windows 使用金鑰免密碼登入 SSH 便學到一個沒聽過的數位簽名演算法名詞 - Ed25519 (老人只聽過 79979... XD)。後面再玩深一點，冒出來的名詞更多，DSA、ECC、Curve25519... 是時侯該更新知識了。

就從這張 GPG (GNU Privacy Guard, GnuPG，可用來加密及簽章的自由軟體) 建立金鑰的選單說起：

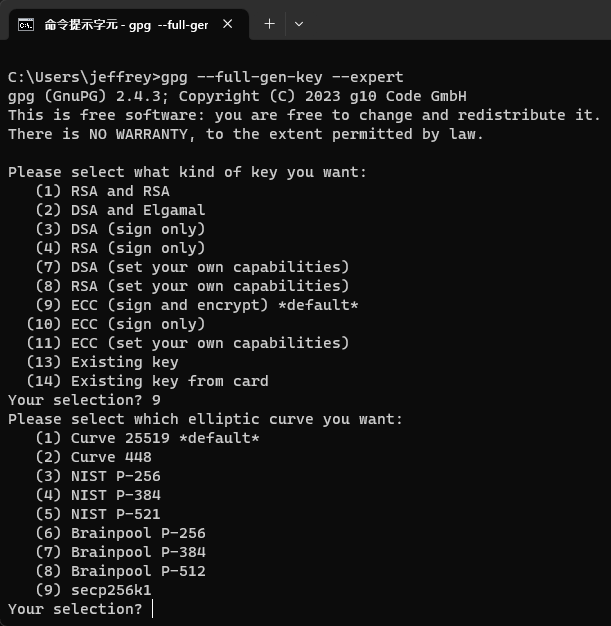
我腦中的非對稱加密演算法只有 RSA，但選單還有 DSA、Elgamal、ECC (我只知道 ECC RAM，Error-Correction Code )，而預設選項是 ECC (sign and encrypt)，代表它是當今的主廚推薦。而 ECC 金鑰又分為 Curve 25519、Curve 448、NIST P-256、NIST P-384、NIST P-521、Brainpool p-256、Brainpool p-384、Brainpool p-512 及 secp256k1，預設值為 Curve 25519。

我把這陣子接觸到的非對稱金鑰相關名詞做個簡單整理：

  1. RSA (Rivest–Shamir–Adleman)
    最早的(也是我當年唯一學過的)公私鑰密碼演算法，原理為整數分解的數學難題，不依賴隨機數產生器(RNG, Random Number Generator)確保來安全性，簽章產生速度慢、驗證快，並可用於加解密，
  2. DSA (Digital Singature Alogrithm)
    NIST(美國國家標準技術研究所) 1991 提出的數位簽章標準，並具有專利，DSA 基於離散對數問題，與 RSA 相比，產生簽名快但驗證慢，用錯 RNG 會破壞安全性。
  3. ECC (Elliptic Curve Cryptograph)
    橢圓曲線密碼學，為橢圓曲線上對映點問題，兩點 T、P 之 T = aP 關聯只能靠窮舉法求解，以 a 為私鑰、T 為公鑰。
  4. 密碼交換 Key Exchange
    在不安全通道上傳送對稱加密金鑰的方法：
    • DHKE(Diffie–Hellman Key Exchange)
      共用基底加入我方祕密交給對方混入其祕密部分，雙方得到相同結果，DHKE 使用離散對數實現，很古老，在 RSA 之前出現
    • ECDH（Elliptic Curve Diffie–Hellman Key Exchange）
      改用橢圓曲線實現 DHKE 交換對稱金鑰
    • ElGamal Encryption Scheme
      埃及密碼學家將 DHKE 延伸成為加密演算法
  5. ECDSA (Elliptic Curve Digital Signature Algorithm)
    橢圓曲線版本的 DSA，比特幣跟以太坊區塊鏈就是使用 ECDSA。ECDSA 可以用較短的金鑰長度達到與 RSA 相同的安全等級(ECDSA 256 bit 接近 RSA 3072 bit)，跟 DSA 一樣，不好的 RNG 會破壞安全性。
    與 RSA/DSA 相比，ECC 簽章小速度快，已漸成當前數位簽章的主流，由 OpenSSH 及 GPG 預設使用 ECC 類型演算法可見一斑：

    圖片來源
  6. EdDSA (Edwards-curve Digital Signature Algorithm)
    基於扭曲愛德華曲線(Twisted Edwards Curve，一種橢圓曲線的平面模型)，效能好且避免 ECDSA 因 RNG 品質不良影響安全性的缺點。
  7. Curve 25519
    Curve25519是一種橢圓曲線，被設計用於 ECDH 可提供 256 Bit 安全金鑰，是無專利保護的高速 ECC 曲線，可用於加密。
  8. Ed25519
    基於 EdDSA 的數位簽章實作，採用 SHA-512/256 及 Curve 25519，安全與安全性比 DSA/ECDSA/EdDSA 更好。OpenSSH 6.5 開始支援。
  9. HMAC (Hash Message Authentication Code)
    驗證內容有無被竄改，原理為對內容計算雜湊值後用私鑰加密產生 MAC；接收方用金鑰解密 MAC 取得雜湊值，與對內容計算雜湊值比對，若二者一致即證明內容未經修改。
  10. NIST 曲線
    GPG 支援的 NIST P-256、NIST P-384、NIST P-521 是美國國家標準技術研究所推出的曲線協議標準，業界懷疑 NSA(美國國家安全局)在 RNG 放入後門，可用來推算私鑰。
  11. Brainpool 曲線
    歐洲擔心 NIST 曲線有漏洞，推出了 Brainpool 曲線標準，GPG 支援 Brainpool p-256、Brainpool p-384、Brainpool p-512
  12. secp256k1
    比特幣使用的 ECDSA 公鑰標準，採用 secp256k1 橢圓曲線。secp256k1 是 SECG (Standards for Efficient Cryptography Group) 推出的標準，與 secp256r1 相比較不受 NIST 影響，後門疑慮較低。

【小結】

  1. 公私鑰密碼學如今已是 ECC 的天下，金鑰短、運算速度快，RSA 的優勢是支援度較廣
  2. ECC 數位簽章標準有很多選擇，ECDSA (NIST P-nnn) 存在 NSA 在 RNG 亂數產生器埋後門的疑慮、EdDSA 無專利問題且不會因 RNG 不良破壞安全性
  3. 不像 RSA 可同時加密及簽章，EdDSA 使用 Curve25519 加解密、Ed25519 製作簽章
  4. 不同領域偏好的簽章標準不同，OpenSSH/GPG 偏好 Ed25519、比特幣等區塊鏈技術多選擇 secp256k1

【參考資料】


Comments

# by Anonymous

瞬間就好專業 不虧是黑大

Post a comment