Coding4Fun - CRC 檢查碼除法演算

CRC 檢查碼我們每天都在用，Ethernet 乙太網路的每個封包(Frame)後方有個 FCS (Frame Check Sequence)，可以用來偵測傳輸過程有沒有 0 變成 1、1 變成 0 的錯誤。其使用的演算法為 Cyclic Redundancy Check 循環冗餘校驗，簡稱 CRC。

來源：維基百科 Ethernet Frame

這玩意兒在網路的很底層被處理掉，用來確保最基本的資料傳輸正確性，我們開發一般應用程式不會寫到，甚至不需要搞懂，就像每天儘量按馬桶把手沖水享受清潔便利的生活就好，不需要了解下水道怎麼串接，污水處理廠如何運作。

但就研究演算法的角度，這是個趣的題目，搞懂原理還挺有趣的。(每次看完這類演算法，都不禁要佩服數學家的腦袋，怎麼能想出這麼巧妙的解法)

CRC 運算原理網上教學很多(例如：CRC檢查碼編碼)，這裡不多贅述，我對其中有個 Modulo-2 Binary Division (依據 資訊學會電腦名詞譯名，譯為模二二進位除法) 有興趣，其運算規則類似十進位除法，但用 XOR 取代相減，數字不足時不需借位，一般在解說原理時都會手算，如下圖：

圖片來源

看到這裡，大家應該都知道我想做什麼了。是的，身為重度 Coding 成癮者，怎麼放過這個練習機會，當然要寫個程式取代手算囉~

using System.Text.RegularExpressions;
//args = args.Length == 0 ? new[] { "101010100000", "10111" } : args;

if (args.Length < 2)
{
    Console.WriteLine("Syntax: modulo-2-division <dividend> <divisor>");
    Console.WriteLine("Eaxmple: modulo-2-division 1010101 101");
    return;
}
var dividend = args[0];
var divisor = args[1];
var binDigChk = new Regex("^[01]+$");
var msgs = new List<string>();
if (!binDigChk.IsMatch(dividend))
    msgs.Add("dividend must be a binary number");
if (!binDigChk.IsMatch(divisor))
    msgs.Add("divisor must be a binary number");
if (msgs.Count > 0)
{
    Console.WriteLine(string.Join("\n", msgs));
    return;
}
var dividendLen = dividend.Length;
var divisorLen = divisor.Length;
var deltaLen = dividendLen - divisorLen;
msgs.Add(new string(' ', divisorLen) + "+" + new string('-', dividendLen));

// color red, yellow, green, cyan, magenta, blue    
var colorNums = new[] { 31, 33, 32, 36, 35, 34 };
var clrIdx = 0;
Func<int, char, string> colorText = (idx, text) => $"\u001b[{colorNums[idx % colorNums.Length]}m{text.ToString()}\u001b[0m";
Func<int, int, string, string> getPadding = (st, cnt, text) =>
    string.Join(string.Empty, Enumerable.Range(0, cnt).Select(o => colorText(st + o, text == null ? ':' : text[o])).ToArray());

msgs.Add($"{divisor}|{dividend.Substring(0, dividendLen - deltaLen)}{getPadding(0, deltaLen, dividend[divisorLen..])}");

var m = dividend.Substring(0, divisorLen);
var quotient = "";
var indent = new string(' ', divisorLen + 1);
Func<string, string, string> xor = (a, b) =>
    {
        if (a.Length != b.Length)
            throw new ArgumentException("a and b must be the same length");
        return new string(Enumerable.Range(0, a.Length)
            .Select(o => a[o] == b[o] ? '0' : '1').ToArray());
    };

for (var i = 0; i <= deltaLen; i++)
{
    var q = m[0] == '1' ? "1" : "0";
    var p = q == "1" ? divisor : new string('0', divisorLen);
    var remainder = xor(m, p)[1..];
    quotient += q;
    var padding = getPadding(i, deltaLen - i, null!);
    msgs.Add($"{indent}\x1b[38;5;21m{p[..1]}\x1b[0m{p[1..]}{padding}");
    msgs.Add($"{indent}{new string('-', divisorLen)}{padding}");
    indent += " ";
    m = remainder +
        (divisorLen + i < dividend.Length ? dividend.Substring(divisorLen + i, 1) : "");
    if (i < deltaLen)
        msgs.Add($"{indent}{m[..^1]}{colorText(clrIdx++, m[^1])}{getPadding(i + 1, deltaLen - i - 1, null!)}");
    else
        msgs.Add($"{indent}{m}");
}
msgs.Insert(0, $"{new string(' ', divisorLen * 2)}\x1b[38;5;21m{quotient}\x1b[0m");
Console.WriteLine(string.Join("\n", msgs));

邏輯很單純，用程式演練一次手算規則而已，借用昨天說的 ANSI 顏色控制碼技巧，我很假掰地加了彩色數字對齊標線。大部分手算會省略第一碼是 0 的回合，我選擇如實輸出，並將數字標上鮮藍色與商數的每一位對映。

成果如下，薑薑薑講~~~

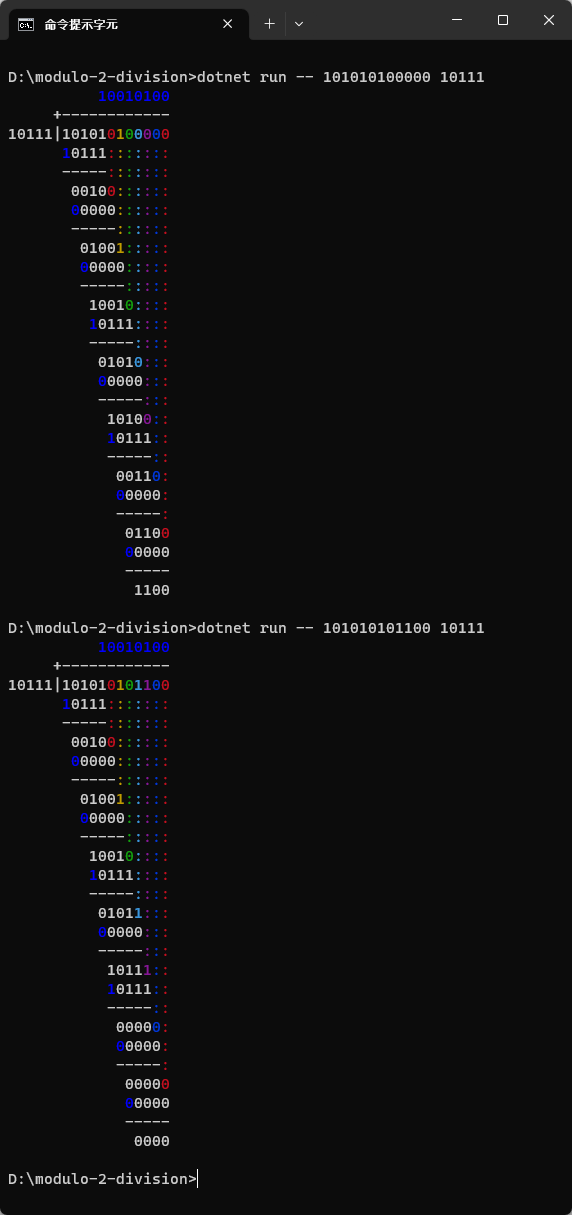
另外，VSCode Intellisense 教我一個新寫法，str.Substring(0, 1) 可以寫成 str[..1]，str.Substring(1) 可寫成 str[1..]，取最後一個字元可以寫 str[^1]，str.Substring(0, str.Length -1) 則可寫成 str[..^1]。寫法相對簡潔，但不熟悉C# 陣列索引範圍語法的話，多看幾次才會習慣，學會活用這個 C# 8 加入的新特性，是本次的額外收獲。

A little C# example to demostrating the modulo 2 divsion calculation of CRC.