Coding4Fun - 小三數學題
| | | 8 | |
在同事的 LINE 群組看到這個據說是小三的趣味數學題(是國小三年級啦,有人是衝著狐狸精才點進來看的嗎?)。
請在下列方格內填入 1-9 的數字以滿足等式:
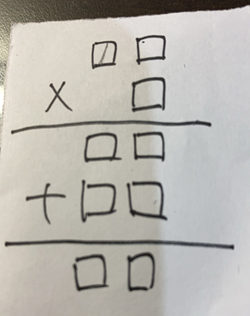
應該可以用相乘、相加不可超過百位數的限制先過濾掉一些組合再嘗試排列求解,BUT...
小孩子才用紙筆,我偏要用 Coding
早上晨跑腦袋閒著開始解題,這個小題目跑遞迴可輕鬆解決,跑著跑著演算法成形,回家連澡都沒洗,急著把程式寫出來,花十分鐘寫好第一個版本:
using System;
namespace MathGame
{
public class Attacker
{
protected bool[] used = new bool[11];
protected byte[] ans = new byte[11];
protected bool printResult = true;
public void Fire(bool print = true)
{
printResult = print;
Explore(1);
}
public virtual void Explore(int pos)
{
if (pos == 10)
{
if (Check() && printResult)
PrintAnswer();
return;
}
for (byte i = 1; i < 10; i++)
{
if (used[i]) continue;
used[i] = true;
ans[pos] = i;
Explore(pos + 1);
used[i] = false;
}
}
public bool Check()
{
if ((ans[1] * 10 + ans[2]) * ans[3] != ans[4] * 10 + ans[5])
return false;
if (ans[4] * 10 + ans[5] + ans[6] * 10 + ans[7] != ans[8] * 10 + ans[9])
return false;
return true;
}
public void PrintAnswer()
{
Console.WriteLine($@"
{ans[1]} {ans[2]}
x {ans[3]}
-----
{ans[4]} {ans[5]}
+ {ans[6]} {ans[7]}
-----
{ans[8]} {ans[9]}");
}
}
}
薑! 薑! 薑! 薑~~ 答案出爐:
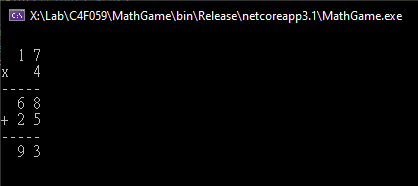
想了一下,有個地方可以改善,排列組合到第五個數字其實就該可先檢查上方的乘法等式,若不相等後面就不用試了,小調一下可省下大量無謂計算,於是我再改了第二個版本:
using System;
namespace MathGame
{
public class AttackerV2 : Attacker
{
public override void Explore(int pos)
{
if (pos == 10)
{
if (ChkAdd() && printResult)
PrintAnswer();
return;
}
for (byte i = 1; i < 10; i++)
{
if (used[i]) continue;
used[i] = true;
ans[pos] = i;
if (pos != 5 || ChkMultiple())
{
Explore(pos + 1);
}
used[i] = false;
}
}
public bool ChkMultiple()
{
if ((ans[1] * 10 + ans[2]) * ans[3] != ans[4] * 10 + ans[5])
return false;
return true;
}
public bool ChkAdd()
{
if (ans[4] * 10 + ans[5] + ans[6] * 10 + ans[7] != ans[8] * 10 + ans[9])
return false;
return true;
}
}
}
既然有改良就該做比較,用 BenchmarkDotNet 測一下:
using BenchmarkDotNet.Attributes;
namespace MathGame
{
public class Tester
{
[Benchmark]
public void TestAttacker()
{
var attacker = new Attacker();
attacker.Fire(false);
}
[Benchmark]
public void TestAttackerV2()
{
var attacker = new AttackerV2();
attacker.Fire(false);
}
}
}
實測結果,用 Core i5 暴力攻擊解這個小三數學問題是大砲打小鳥無誤,無腦攻擊版只花了 15.94ms,而簡單改良省去部分無效計算後更是再提升到 0.26ms:
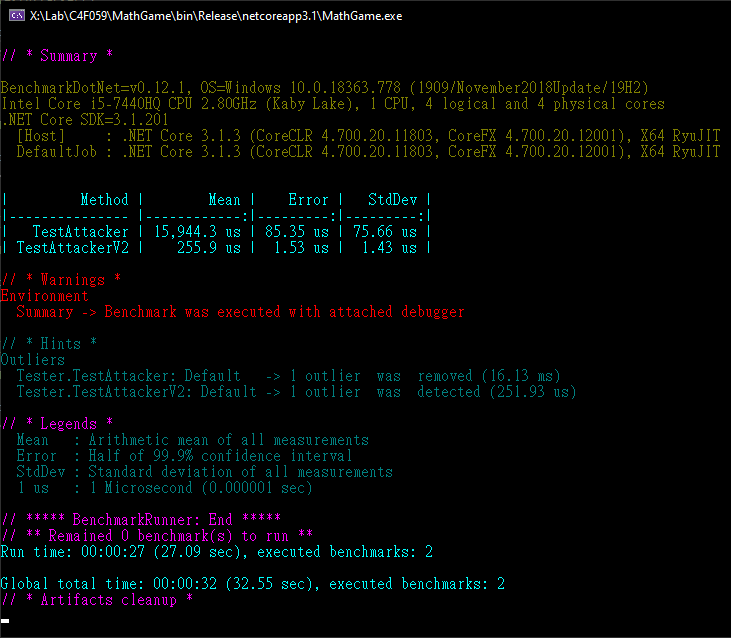
演算法是否還有優化空間?當然有,但花時間改善耗時 0.26ms 的計算投資報酬率實在太低,就此打住。
2020-05-09 更新:原本程式有 Bug,只算到第八個數字就當成結束,故組合中會出現 0 而 1-9 缺一個。天大的 Bug! 謝謝讀者 wilber, 吳 提醒。(掩面)
For fun, I write a C# recursive function to solve a math question of primary school.
Comments
# by wilber
不是說1-9嗎?0怎麼來的?XDDD
# by 吳
總共9個位置。但是他用0-9 會有一個用不到。第一個缺8第二個缺7第三個缺5
# by Jeffrey
to wilber, 吳,哈,太丟臉了! 這麼大的Bug,馬上修正。
# by FAT
這個有python版本的嗎?
# by Jeffrey
to FAT, 來學 C# 吧! 很好玩的。這裡有線上版 https://dotnetfiddle.net/IduX74 (硬要推坑)
# by Vincent
from itertools import permutations def check(x): if ((x[0]*10+x[1])*x[2] == x[3]*10+x[4]): if (((x[3]*10+x[4]) + (x[5]*10+x[6])) == x[7]*10+x[8]) : print (x) perm = permutations([1,2,3,4,5,6,7,8,9]) for i in list(perm): check(i) 以上是 Python 版. 其實最難是做排列的演算法. 站在巨人的臂上就不用思考了:)
# by Jeffrey
to Vincent, 噗,也太省事了。讚!
# by B
提供給你一個想法. AttackerV2 attackerV2 = new AttackerV2(); attackerV2.Explore(int.MaxValue); 我相信你知道會發生什麼事了!