浮點數計算結果更接近正解？

讀者 Lina 問了一個有趣問題：

為什麼 float 計算 193.25*4/3*3 等於 773 跟手算結果相同(除 3 跟乘 3 可約分)，用 decimal 計算 193.25*4/3*3 卻是 773.00000000000000000000000001 反而誤差更大？

依據黑大名言「算錢用浮點，遲早被人扁」要精準當用 decimal，為何這回 decimal 輸給 float？黑大被打臉了嗎？

經過實測，以上算式用 decimal 的確會多出 0.00000000000000000000000001，用 float 反而不會：(註：在數字後方加上 f、d、m 結尾 可宣告常數為 float、double 或 decimal 型別)

Console.WriteLine(193.25f*4f/3f*3f);
Console.WriteLine(193.25m*4m/3m*3m);

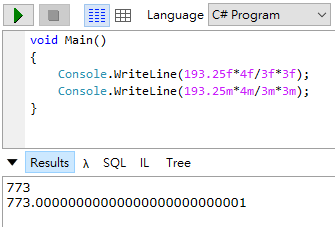
改寫成較簡單的例子，用 1/3*3 也能重現問題：

Console.WriteLine(1f/3f*3f);
Console.WriteLine(1m/3m*3m);

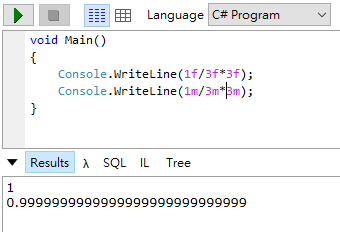
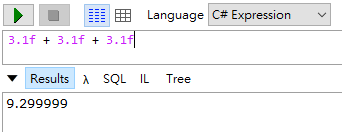
嚴格來說，float、double 與 decimal 都是浮點數，但 float、double 與 decimal 的實作方式不同。float 與 double 為二進位浮點數(Binary Floating-Pont Format)、decimal 為十進位浮點數(Decimal Floating-Point Format)，二者特性差蠻多的，而我慣稱的「浮點數」應是指 float、double 這類二進位浮點數(浮點數中文維基百科也只涵蓋了 float 及 double)，我沒鑽研過原理(也不想鑽研，一點也不有趣呀)，但約略知道二進位浮點數採近似值的概念。當你設定浮點數變數為 0.1，實際存入電腦記憶體的二進位值其實等於 0.100000001490116119384765625 而非 0.1，故計算過程常會失去精度，其加法與乘法亦不符合結合律與分配律 參考。這個例子只是恰巧 float 計算值更接近數學預期結果，並不代表它比較準確。1/3*3 = 1 跟 3.1f+3.1f+3.1f=9.299999 一樣都是近似誤差造成，只是前者歪打正著意外命中目標，雖然討喜，卻不值得讚許。

我再加入一些變化計算，以突顯浮點數跟 decimal 的行為差異：

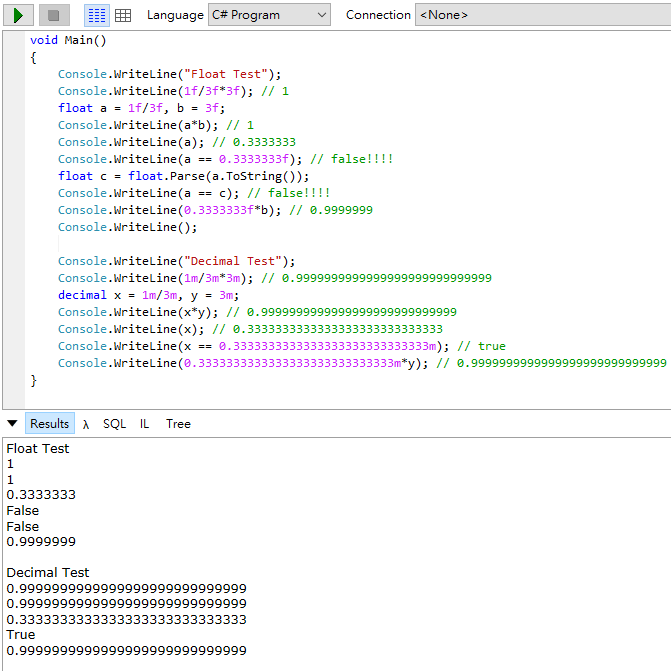
最精彩的部分在這裡：

float a = 1/3，a 值顯示為 0.3333333，雖然 a * 3 會等於 1，BUT!

a 不等於 0.3333333f

a 不等於 float.Parse(a.ToString())

你可以想像成 a 是一個趨近 0.3333333 但不等於 0.3333333 的值，精準數值沒人知道，因此你無法 100% 預期它的結果。相較之下，decimal 可靠許多：

1 / 3 * 3 等於 0.9999999999999999999999999999
若 x = 1 / 3，則 x 等於 0.3333333333333333333333333333m
x * 3 = 0.9999999999999999999999999999

你永遠可以預期 decimal 每次計算與比對的結果，在需要精確掌握結果的場合，decimal 遠比 float/double 更值得信賴。

回到最開始的問題上，float 計算結果等於數學上的正確答案是種「美麗的錯誤」，並不代表它比較精準，同樣誤差若發生在其他場合很可能讓你笑不出來；decimal 畢竟儲存位數有限，遇到循環小數就必須四捨五入到最小位數(就像數位照片解析度再高，還是回歸以像素為單位儘可能描繪實景)，故與數學正解有差距在意料之內，但差距可以被解釋也能被預期，應列為系統規格的一部分。一般常見做法是事先約定無法除盡時四捨五入到小數第幾位，只要確保每次遇到相同情況結果一致就不會有爭議。

最後，請大家一起跟我複誦

算錢用浮點，遲早被人扁

若對數字精準度要求很高，不想計算比對結果充滿「驚喜」，請愛用 decimal。

Some cases to explain why you should not use float when pricision is important.