再探 Double 浮點數等於地雷
 |  | 0 |  |  |
同事分享地雷一枚。先踩到 ODP.NET OracleDataReader 數字型別對映陷阱,未指定 decimal 交由 ODP.NET 自由決定,某個 NUMBER(10, 2) 欄位被轉成 double,生出 1519222.6099999999 這種浮點數字,之後再陷入數字到底是 .609999... 還是 .61 的迷惑中。(「算錢用浮點,遲早被人扁」啊,各位)
查了文件,到 ODP.NET 21.x 都是依數字長度及小數位數採用不同型別,實測 Managed ODP.NET 則一律轉為 decimal,算是把坑埋起來了,用 Managed ODP.NET 不必再擔心踩雷。但 double 有時是 .609999... 有時變 .61,搞到自己不等於自己的狀況仍存在,我用以下範例重現問題:
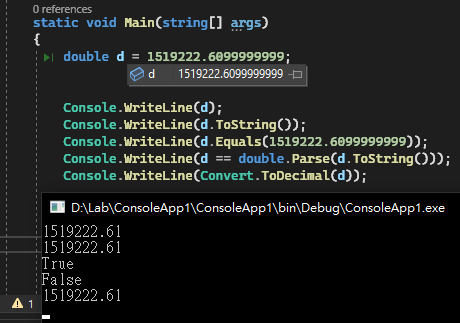
用 Visual Studio 偵錯查到的數字是 1519222.6099999999,但 Console.WriteLine(d) 會得到 1519222.61,ToString() 跟轉型 decimal 也是 .61,還得到一個奇妙的比對結果 d != double.Parse(d.ToString())。
嚴格來說,這是 .NET 實作浮點數運算的邏輯,不同語言的做法不一,像 JavaScript 就是採用原汁原味輸出:
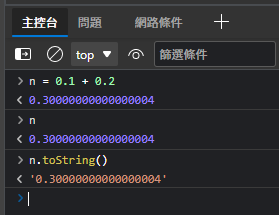
這問題其實上回就有踩到,但當時沒深究。事隔多年再遇上,想必是孽緣,就來追一下 .NET 原始碼,查查為什麼 ToString() 跟轉型 decimal 會得到原始數字。
.NET Source Browser https://source.dot.net/是查詢 .NET 原始碼的好地方,我們可以查出 double.ToString() 背後是靠 Number.FormatDouble() 轉字串:
public override string ToString()
{
return Number.FormatDouble(m_value, null, NumberFormatInfo.CurrentInfo);
}
再追到 Number.FormatDouble(),邏輯遠比想像複雜,還包含了 Dragon4、Grisu3 等浮點數轉字串演算法,這塊涉及博士論文等級的學術研究,水很深,我就不潛進去了。但約略可知,C# 在 double.ToString() 會使用預設的精準位數四捨五入(猜測應是 DoublePrecisionCustomFormat = 15),因此 1519222.6099999999 會被轉成 1519222.61。
/// <summary>Formats the specified value according to the specified format and info.</summary>
/// <returns>
/// Non-null if an existing string can be returned, in which case the builder will be unmodified.
/// Null if no existing string was returned, in which case the formatted output is in the builder.
/// </returns>
private static unsafe string? FormatDouble(ref ValueStringBuilder sb, double value, ReadOnlySpan<char> format, NumberFormatInfo info)
{
if (!double.IsFinite(value))
{
if (double.IsNaN(value))
{
return info.NaNSymbol;
}
return double.IsNegative(value) ? info.NegativeInfinitySymbol : info.PositiveInfinitySymbol;
}
char fmt = ParseFormatSpecifier(format, out int precision);
byte* pDigits = stackalloc byte[DoubleNumberBufferLength];
if (fmt == '\0')
{
// For back-compat we currently specially treat the precision for custom
// format specifiers. The constant has more details as to why.
precision = DoublePrecisionCustomFormat;
}
NumberBuffer number = new NumberBuffer(NumberBufferKind.FloatingPoint, pDigits, DoubleNumberBufferLength);
number.IsNegative = double.IsNegative(value);
// We need to track the original precision requested since some formats
// accept values like 0 and others may require additional fixups.
int nMaxDigits = GetFloatingPointMaxDigitsAndPrecision(fmt, ref precision, info, out bool isSignificantDigits);
if ((value != 0.0) && (!isSignificantDigits || !Grisu3.TryRunDouble(value, precision, ref number)))
{
Dragon4Double(value, precision, isSignificantDigits, ref number);
}
number.CheckConsistency();
// When the number is known to be roundtrippable (either because we requested it be, or
// because we know we have enough digits to satisfy roundtrippability), we should validate
// that the number actually roundtrips back to the original result.
Debug.Assert(((precision != -1) && (precision < DoublePrecision)) || (BitConverter.DoubleToInt64Bits(value) == BitConverter.DoubleToInt64Bits(NumberToDouble(ref number))));
if (fmt != 0)
{
if (precision == -1)
{
Debug.Assert((fmt == 'G') || (fmt == 'g') || (fmt == 'R') || (fmt == 'r'));
// For the roundtrip and general format specifiers, when returning the shortest roundtrippable
// string, we need to update the maximum number of digits to be the greater of number.DigitsCount
// or DoublePrecision. This ensures that we continue returning "pretty" strings for values with
// less digits. One example this fixes is "-60", which would otherwise be formatted as "-6E+01"
// since DigitsCount would be 1 and the formatter would almost immediately switch to scientific notation.
nMaxDigits = Math.Max(number.DigitsCount, DoublePrecision);
}
NumberToString(ref sb, ref number, fmt, nMaxDigits, info);
}
else
{
Debug.Assert(precision == DoublePrecisionCustomFormat);
NumberToStringFormat(ref sb, ref number, format, info);
}
return null;
}
若非看到 .6099999999 不可,可以寫 ToString("G17") 將精準度拉到 17 位(預設為 15 位):
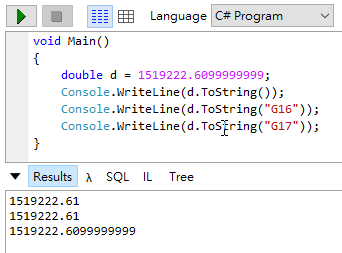
至於 (decimal) dobuleValue,則會套用 new decimal(value):
public static explicit operator decimal(double value) => new decimal(value);
// Constructs a Decimal from a double value.
//
public Decimal(double value)
{
DecCalc.VarDecFromR8(value, out AsMutable(ref this));
}
而 DecCalc.VarDecFromR8 會四捨五入取 15 位 (Round the input to a 15-digit integer. The R8 format has only 15 digits of precision, and we want to keep garbage digits out of the Decimal were making.) 故得到結果與 ToString() 一樣是 .61。
回到 ToString() 該輸出 .6099999999 還是 .61 這件事上。不管哪種結果是取捨的結果,C# 採行做法的好處是程式不會印出 0.1 + 0.2 = 0.30000000000000004 這種結果。
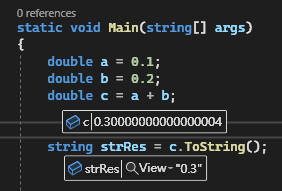
而 ToString() 選擇貼近原始值而非呈現浮點精準數字,無法避免地導致 double.Parse(d.ToString()) != d,想當然會引來正反不同意見,例如這篇 Don't use double.ToString() if you don't want to lose precision。
問我的看法? 別再糾結 double 的特殊行為了,浮點數不是這樣用滴,需精準到數字一位不差的場合,用 decimal 讓自己的人生好過一些吧!
Tracing .NET source code to find why double.ToString() returns rounded result.
Comments
Be the first to post a comment