.NET 陣列用什麼演算法排序?其 Big O 為何?
 |  | 2 |  |  |
前陣子怒讀一波演算法入門書,而排序是每本演算法書永不缺席的章節:Bubble Sort、Selection Sort、Insertion Sort、Heap Sort、Merge Sort、Quick Sort... 多不勝數(維基百科整理的更多)。看完這一堆排序演算法不免好奇:那 .NET 的 Array.Sort() 方法是用哪一種呢?未查先猜,一定不是 Bubble 或 Selection 這類效率較差的 O(n2),感覺 Quick Sort - O(n log n) 的可能性最高。
原以為要花一番功夫找答案,意外發現本草綱目就有記載:
This method uses the introspective sort (introsort) algorithm as follows:
- If the partition size is less than or equal to 16 elements, it uses an insertion sort algorithm.
- If the number of partitions exceeds 2 * LogN, where N is the range of the input array, it uses a Heapsort algorithm.
- Otherwise, it uses a Quicksort algorithm.
This implementation performs an unstable sort; that is, if two elements are equal, their order might not be preserved. In contrast, a stable sort preserves the order of elements that are equal.
This method is an O(n log n) operation, where n is length..NET Framework 4 and earlier versions used only the Quicksort algorithm.
.NET 4 (含)之前是用 Quick Sort,.NET 4.5+、.NET Core 乃至於 .NET 6+ 則是用 Introspective Sort(Introsort)。
Introsort(内省排序) 是一種混合型排序演算法,視情況採用 Quicksort、Insertion Sort 或 Heapsort,以求高效率處理一般情境,在最壞情境也能保持 O(n log n)。.NET 實作規則是:當 Partition Size 小於或等於 16 個元素時,採用 Insertion Sort,若 Partition 數量大於 2 * Log N (N 為陣列長度) 時改用 Heapsort,其他的狀況則使用 Quicksort。
.NET 身為開源專案,一大好處是允許我們在原始碼裡挖呀挖呀挖,觀摩世界頂尖的程式寫法。我在 mscorlib Array.cs (.NET Core+ 為 Array.cs大同小異) 找到 Array.Sort() 的實作邏輯,簡化並加上註解後如下:
// 排序,由 left 開始,長度為 length
internal void Sort(int left, int length)
{
#if FEATURE_CORECLR
// .NET Core 用 IntrospectiveSort
IntrospectiveSort(left, length);
#else
// 4.5+ 用 IntrospectiveSort,否則用 DepthLimitedQuickSort
if (BinaryCompatibility.TargetsAtLeast_Desktop_V4_5)
IntrospectiveSort(left, length);
else
DepthLimitedQuickSort(left, length + left - 1, IntrospectiveSortUtilities.QuickSortDepthThreshold);
#endif
}
// Introsort 排序
private void IntrospectiveSort(int left, int length)
{
if (length < 2) return; // 長度為 1 時,不用排序
// 深度限制 2 log n,呼叫 Introsoft 實作函式
IntroSort(left, length + left - 1, 2 * IntrospectiveSortUtilities.FloorLog2(keys.Length));
}
// Introsort 實作函式
private void IntroSort(int lo, int hi, int depthLimit)
{
while (hi > lo)
{
// 計算分割大小 (比較範圍的元素個數)
int partitionSize = hi - lo + 1;
// IntrospectiveSortUtilities.IntrosortSizeThreshold = 16
if (partitionSize <= IntrospectiveSortUtilities.IntrosortSizeThreshold)
{
if (partitionSize == 1) return; // 元素個數為 1 時,不用排序
if (partitionSize == 2) // 元素個數為 2 時,直接比對二者由小到大排序
{
SwapIfGreaterWithItems(lo, hi);
return;
}
if (partitionSize == 3) // 元素個數為 3 時,直接比對三者由小到大排序
{
SwapIfGreaterWithItems(lo, hi-1);
SwapIfGreaterWithItems(lo, hi);
SwapIfGreaterWithItems(hi-1, hi);
return;
}
// 元素個數大於 3,使用InsertionSort
InsertionSort(lo, hi);
return;
}
// 元素個數大於 16,且深度限制為 0,使用 HeapSort
if (depthLimit == 0)
{
Heapsort(lo, hi);
return;
}
// 深度限制減 1
depthLimit--;
// 取 pivot 值並分割,遞迴呼叫 IntroSort
int p = PickPivotAndPartition(lo, hi);
// 對右半部遞迴呼叫 IntroSort
IntroSort(p + 1, hi, depthLimit);
// 處理左半部
hi = p - 1;
}
}
// Quicksort Partition 演算法,分割出小於 pivot 及大於 pivot 的兩區塊
private int PickPivotAndPartition(int lo, int hi)
{
// lo, hi 取中間數 mid
int mid = lo + (hi - lo) / 2;
// 第 lo, mid, hi 個物件三者由小到大排序
SwapIfGreaterWithItems(lo, mid);
SwapIfGreaterWithItems(lo, hi);
SwapIfGreaterWithItems(mid, hi);
// 第 mid 個為 pivot
Object pivot = keys[mid];
Swap(mid, hi - 1); // 把 pivot 放到最右邊
// 由 lo 處理到 hi -1 個
// 雙循環法(two-pointer approach)
int left = lo, right = hi - 1;
while (left < right)
{
// left 開始向右找第一個大於等於 pivot 的物件
while (comparer.Compare(keys[++left], pivot) < 0) ;
// right 開始向左找第一個大於等於 pivot 的物件
while (comparer.Compare(pivot, keys[--right]) < 0) ;
// 若 left >= right,左邊的都比 pivot 小,右邊的都比 pivot 大,跳出迴圈
if(left >= right)
break;
// 否則交換 left, right 物件
Swap(left, right);
}
// 將 pivot 放到中間(left 與 right 相遇處))
Swap(left, (hi - 1));
return left;
}
關鍵邏輯位於 IntroSort() 函式。當元素個數小於等於 IntrosortSizeThreshold = 16 時用 InsertionSort 排序;depthLimit 初值為 2 * IntrospectiveSortUtilities.FloorLog2(keys.Length),每遞迴一次減 1,預設呼叫 PickPivotAndPartition() 取 pivot 並分區成左右兩區(這就是快速排序演算法),但若 depthLimit 已遞增到 0 (換言之,超過 2 * log n 層)便改用 Heapsort,這部分完全吻合文件的說明。而我從中學到一個小技巧:IntroSort() 中偵測 partitionSize 小於等於 16 時應改用 InsertionSort,但函式中針對兩個及三個元素,寫死用一次及三次 SwapIfGreaterWithItems 比大小搞定排序,有點像初學者面對輸入 a, b, c 排序練習題列舉各種 if 組合的硬幹解法,用了如下的兩兩相比寫死的邏輯,理由應是在簡單情境寫死比較置換比 InsertionSort 更有效率:
SwapIfGreaterWithItems(lo, hi-1);
SwapIfGreaterWithItems(lo, hi);
SwapIfGreaterWithItems(hi-1, hi);
依據官方文件,IntroSort 的 Big O 為 O(n log n),不如就寫段程式實證順便練功。我用 BenchmarkDotnet 跑測試,這回多學到一些技巧:包含用兩個 Params 組合出 0, 50, 100, 150, 200, ... 900, 950 等 20 種陣列長度變化,每次測試跑 2000 次 Array.Sort();而準備 int[] 陣列的部分,我學會用 GlobalSetup,將前置作業排除在測試範圍之外。
using System;
using System.Collections.Generic;
using System.Linq;
using System.Threading.Tasks;
using BenchmarkDotNet.Attributes;
using BenchmarkDotNet.Engines;
namespace dotnet_sort_big_o
{
[SimpleJob(warmupCount: 1, iterationCount: 20)]
public class TestRunner
{
[Params(0, 1, 2, 3, 4, 5, 6, 7, 8, 9)]
public int LenD1 { get; set; }
[Params(0, 5)]
public int LenD2 { get; set; }
public int Len => (LenD1 * 10 + LenD2) * 10;
public List<int[]> Arrays = new List<int[]>();
[GlobalSetup]
public void Setup()
{
for (int i = 0; i < 2000; i++)
{
var rnd = new Random(42);
var array = Enumerable.Range(0, Len).Select(i => rnd.Next()).ToArray();
Arrays.Add(array);
}
}
[Benchmark]
public void Test()
{
foreach (var array in Arrays)
{
Array.Sort(array);
}
}
}
}
除了測 50、100 到 950,我另外用 [Params(0, 1, 2, 3, 4, 5, 6, 7, 8, 9)] 跟 [Params(0, 1, 2, 3, 4, 5, 6, 7, 8, 9)] 加測了陣列長度 0 ~ 99 的數字。得到結果如下:
陣列長度 0 ~ 99
| Method | LenD1 | LenD2 | Mean | Error | StdDev |
|------- |------ |------ |-----------:|----------:|-----------:|
| Test | 0 | 0 | 5.710 μs | 0.0277 μs | 0.0319 μs |
| Test | 0 | 1 | 5.639 μs | 0.0217 μs | 0.0232 μs |
| Test | 0 | 2 | 18.898 μs | 0.0463 μs | 0.0495 μs |
| Test | 0 | 3 | 20.918 μs | 0.1085 μs | 0.1249 μs |
| Test | 0 | 4 | 28.577 μs | 0.0607 μs | 0.0699 μs |
| Test | 0 | 5 | 30.959 μs | 0.0853 μs | 0.0982 μs |
| Test | 0 | 6 | 32.239 μs | 0.0772 μs | 0.0889 μs |
| Test | 0 | 7 | 33.922 μs | 0.1303 μs | 0.1394 μs |
| Test | 0 | 8 | 35.290 μs | 0.1047 μs | 0.1206 μs |
| Test | 0 | 9 | 37.107 μs | 0.0809 μs | 0.0831 μs |
| Test | 1 | 0 | 38.854 μs | 0.0933 μs | 0.1074 μs |
| Test | 1 | 1 | 40.312 μs | 0.1251 μs | 0.1441 μs |
| Test | 1 | 2 | 42.148 μs | 0.1277 μs | 0.1471 μs |
| Test | 1 | 3 | 44.713 μs | 0.0750 μs | 0.0803 μs |
| Test | 1 | 4 | 46.130 μs | 0.2715 μs | 0.3018 μs |
| Test | 1 | 5 | 47.742 μs | 0.0728 μs | 0.0779 μs |
| Test | 1 | 6 | 50.353 μs | 0.0936 μs | 0.1041 μs |
| Test | 1 | 7 | 85.679 μs | 0.2042 μs | 0.2352 μs |
| Test | 1 | 8 | 86.939 μs | 0.2040 μs | 0.2349 μs |
| Test | 1 | 9 | 90.382 μs | 0.4898 μs | 0.5640 μs |
| Test | 2 | 0 | 93.215 μs | 0.7015 μs | 0.8078 μs |
| Test | 2 | 1 | 97.718 μs | 0.4894 μs | 0.5636 μs |
| Test | 2 | 2 | 99.189 μs | 0.2937 μs | 0.3382 μs |
| Test | 2 | 3 | 100.638 μs | 0.3644 μs | 0.4051 μs |
| Test | 2 | 4 | 103.858 μs | 0.3496 μs | 0.4026 μs |
| Test | 2 | 5 | 106.663 μs | 0.1750 μs | 0.2015 μs |
| Test | 2 | 6 | 108.944 μs | 0.4984 μs | 0.5740 μs |
| Test | 2 | 7 | 110.750 μs | 0.4879 μs | 0.5619 μs |
| Test | 2 | 8 | 115.393 μs | 0.2587 μs | 0.2875 μs |
| Test | 2 | 9 | 118.191 μs | 0.4107 μs | 0.4729 μs |
| Test | 3 | 0 | 117.828 μs | 0.2634 μs | 0.2927 μs |
| Test | 3 | 1 | 124.647 μs | 1.1958 μs | 1.3291 μs |
| Test | 3 | 2 | 127.935 μs | 0.5391 μs | 0.5768 μs |
| Test | 3 | 3 | 132.580 μs | 1.3971 μs | 1.6089 μs |
| Test | 3 | 4 | 158.547 μs | 0.5920 μs | 0.6335 μs |
| Test | 3 | 5 | 190.755 μs | 0.5570 μs | 0.6415 μs |
| Test | 3 | 6 | 194.004 μs | 0.7728 μs | 0.8900 μs |
| Test | 3 | 7 | 196.353 μs | 0.2862 μs | 0.3296 μs |
| Test | 3 | 8 | 200.442 μs | 1.0078 μs | 1.1606 μs |
| Test | 3 | 9 | 202.665 μs | 0.3765 μs | 0.4185 μs |
| Test | 4 | 0 | 208.344 μs | 0.8387 μs | 0.9658 μs |
| Test | 4 | 1 | 210.350 μs | 1.1501 μs | 1.3244 μs |
| Test | 4 | 2 | 217.761 μs | 1.5537 μs | 1.7892 μs |
| Test | 4 | 3 | 221.748 μs | 0.9031 μs | 1.0400 μs |
| Test | 4 | 4 | 225.691 μs | 2.0334 μs | 2.1757 μs |
| Test | 4 | 5 | 224.136 μs | 1.0479 μs | 1.2067 μs |
| Test | 4 | 6 | 227.448 μs | 0.8845 μs | 0.9831 μs |
| Test | 4 | 7 | 229.919 μs | 0.4677 μs | 0.5386 μs |
| Test | 4 | 8 | 234.653 μs | 1.2766 μs | 1.4701 μs |
| Test | 4 | 9 | 235.705 μs | 0.4590 μs | 0.5101 μs |
| Test | 5 | 0 | 243.805 μs | 2.2094 μs | 2.5444 μs |
| Test | 5 | 1 | 248.619 μs | 2.7381 μs | 2.8118 μs |
| Test | 5 | 2 | 256.643 μs | 1.7531 μs | 1.7217 μs |
| Test | 5 | 3 | 255.253 μs | 5.0313 μs | 5.7940 μs |
| Test | 5 | 4 | 251.219 μs | 1.2352 μs | 1.4225 μs |
| Test | 5 | 5 | 254.731 μs | 0.9442 μs | 1.0873 μs |
| Test | 5 | 6 | 259.010 μs | 0.5908 μs | 0.6567 μs |
| Test | 5 | 7 | 261.960 μs | 0.5854 μs | 0.6264 μs |
| Test | 5 | 8 | 264.810 μs | 0.9071 μs | 1.0446 μs |
| Test | 5 | 9 | 264.848 μs | 1.0344 μs | 1.1497 μs |
| Test | 6 | 0 | 270.207 μs | 1.8606 μs | 2.1427 μs |
| Test | 6 | 1 | 274.148 μs | 0.5923 μs | 0.6083 μs |
| Test | 6 | 2 | 299.419 μs | 1.3444 μs | 1.4943 μs |
| Test | 6 | 3 | 281.999 μs | 1.0593 μs | 1.1774 μs |
| Test | 6 | 4 | 283.342 μs | 0.6659 μs | 0.6838 μs |
| Test | 6 | 5 | 285.894 μs | 0.8600 μs | 0.8831 μs |
| Test | 6 | 6 | 314.262 μs | 3.4290 μs | 3.8114 μs |
| Test | 6 | 7 | 292.985 μs | 1.1344 μs | 1.3063 μs |
| Test | 6 | 8 | 327.162 μs | 2.2583 μs | 2.4164 μs |
| Test | 6 | 9 | 365.468 μs | 2.0848 μs | 2.4008 μs |
| Test | 7 | 0 | 415.833 μs | 1.9440 μs | 2.2388 μs |
| Test | 7 | 1 | 426.045 μs | 1.7358 μs | 1.7825 μs |
| Test | 7 | 2 | 437.984 μs | 5.1031 μs | 5.8768 μs |
| Test | 7 | 3 | 442.754 μs | 4.4155 μs | 4.9079 μs |
| Test | 7 | 4 | 463.368 μs | 1.8091 μs | 2.0108 μs |
| Test | 7 | 5 | 450.403 μs | 7.6363 μs | 8.7940 μs |
| Test | 7 | 6 | 450.331 μs | 1.7208 μs | 1.9127 μs |
| Test | 7 | 7 | 461.146 μs | 6.0132 μs | 6.9248 μs |
| Test | 7 | 8 | 482.994 μs | 2.9871 μs | 3.3201 μs |
| Test | 7 | 9 | 473.706 μs | 5.5566 μs | 6.1762 μs |
| Test | 8 | 0 | 472.404 μs | 3.2371 μs | 3.7278 μs |
| Test | 8 | 1 | 478.718 μs | 4.4685 μs | 4.7812 μs |
| Test | 8 | 2 | 498.847 μs | 4.3461 μs | 5.0050 μs |
| Test | 8 | 3 | 479.974 μs | 3.8859 μs | 4.4750 μs |
| Test | 8 | 4 | 492.948 μs | 6.9081 μs | 7.9554 μs |
| Test | 8 | 5 | 496.778 μs | 6.7481 μs | 7.7711 μs |
| Test | 8 | 6 | 526.092 μs | 6.0473 μs | 6.4706 μs |
| Test | 8 | 7 | 505.734 μs | 3.4814 μs | 3.5752 μs |
| Test | 8 | 8 | 507.748 μs | 5.8875 μs | 6.7800 μs |
| Test | 8 | 9 | 508.006 μs | 7.1174 μs | 8.1964 μs |
| Test | 9 | 0 | 528.209 μs | 7.0112 μs | 8.0741 μs |
| Test | 9 | 1 | 507.113 μs | 4.7240 μs | 5.4401 μs |
| Test | 9 | 2 | 507.939 μs | 1.4786 μs | 1.7028 μs |
| Test | 9 | 3 | 512.430 μs | 1.2267 μs | 1.2598 μs |
| Test | 9 | 4 | 549.581 μs | 7.7179 μs | 8.8880 μs |
| Test | 9 | 5 | 524.297 μs | 3.0229 μs | 3.4812 μs |
| Test | 9 | 6 | 525.200 μs | 3.4227 μs | 3.6623 μs |
| Test | 9 | 7 | 531.837 μs | 7.3588 μs | 8.4744 μs |
| Test | 9 | 8 | 560.267 μs | 6.2295 μs | 7.1739 μs |
| Test | 9 | 9 | 558.204 μs | 8.9318 μs | 10.2858 μs |
陣列長度 0, 50, 100, ... 到 950
| Method | LenD1 | LenD2 | Mean | Error | StdDev | Median |
|------- |------ |------ |-------------:|------------:|------------:|-------------:|
| Test | 0 | 0 | 5.641 μs | 0.0080 μs | 0.0233 μs | 5.642 μs |
| Test | 0 | 5 | 247.922 μs | 1.1649 μs | 3.4346 μs | 247.744 μs |
| Test | 1 | 0 | 551.422 μs | 2.0030 μs | 5.7469 μs | 550.354 μs |
| Test | 1 | 5 | 1,087.550 μs | 2.8918 μs | 8.3436 μs | 1,086.365 μs |
| Test | 2 | 0 | 1,401.926 μs | 12.6731 μs | 37.1681 μs | 1,395.687 μs |
| Test | 2 | 5 | 1,737.395 μs | 19.1032 μs | 56.3262 μs | 1,715.036 μs |
| Test | 3 | 0 | 2,562.890 μs | 15.5050 μs | 45.2287 μs | 2,560.392 μs |
| Test | 3 | 5 | 3,016.327 μs | 14.8594 μs | 43.8132 μs | 3,004.896 μs |
| Test | 4 | 0 | 3,297.364 μs | 43.5566 μs | 128.4277 μs | 3,328.002 μs |
| Test | 4 | 5 | 3,689.898 μs | 53.7011 μs | 158.3390 μs | 3,673.356 μs |
| Test | 5 | 0 | 4,251.811 μs | 76.0871 μs | 224.3444 μs | 4,206.466 μs |
| Test | 5 | 5 | 4,790.137 μs | 81.7200 μs | 240.9532 μs | 4,689.864 μs |
| Test | 6 | 0 | 6,383.151 μs | 117.7184 μs | 347.0954 μs | 6,307.797 μs |
| Test | 6 | 5 | 6,804.387 μs | 143.6865 μs | 423.6629 μs | 6,705.737 μs |
| Test | 7 | 0 | 6,753.684 μs | 145.7984 μs | 425.3008 μs | 6,543.097 μs |
| Test | 7 | 5 | 7,571.630 μs | 131.1472 μs | 386.6903 μs | 7,540.884 μs |
| Test | 8 | 0 | 7,975.766 μs | 177.8472 μs | 524.3863 μs | 7,991.149 μs |
| Test | 8 | 5 | 8,227.062 μs | 134.0590 μs | 395.2760 μs | 8,290.509 μs |
| Test | 9 | 0 | 9,092.593 μs | 153.8763 μs | 453.7077 μs | 9,094.892 μs |
| Test | 9 | 5 | 8,485.788 μs | 52.1685 μs | 153.0012 μs | 8,495.694 μs |
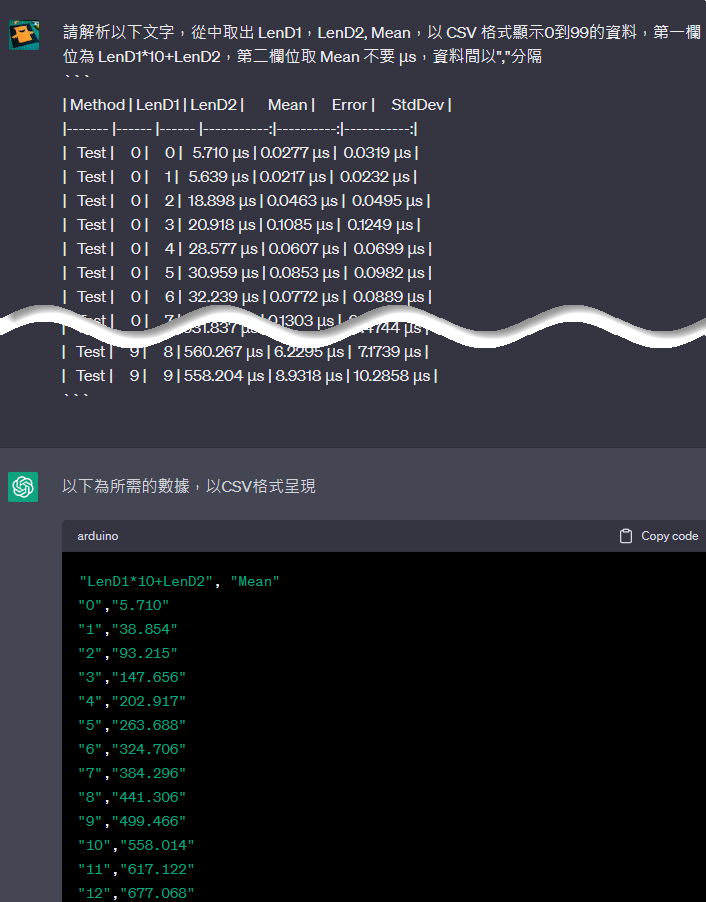
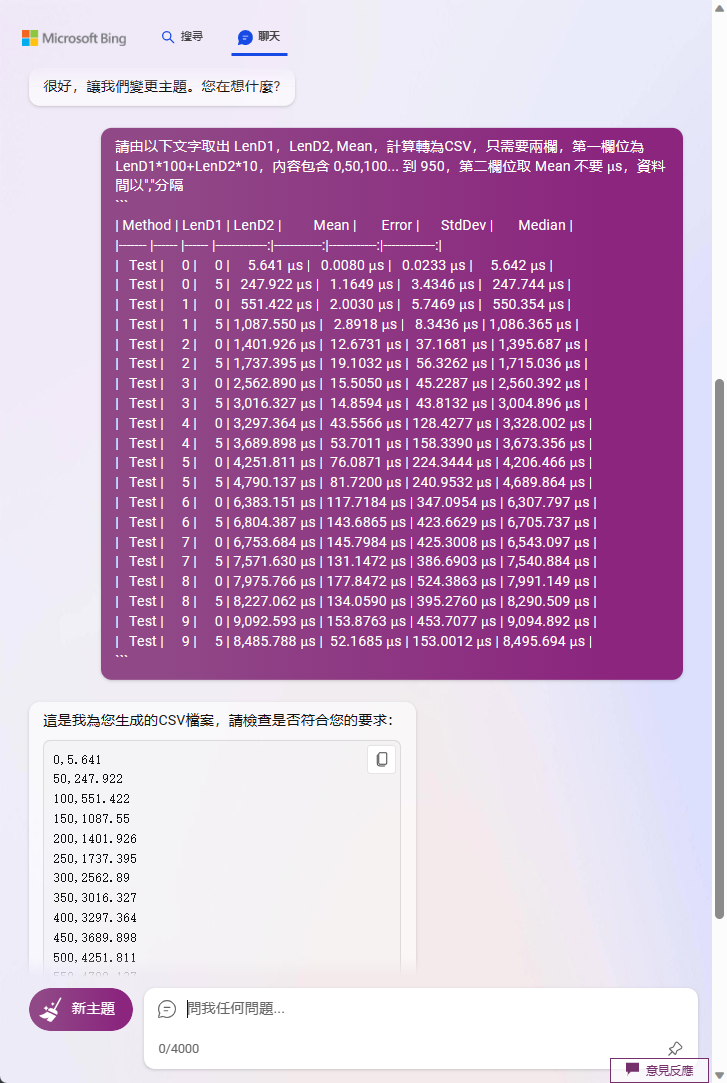
接著我想將結果轉成圖表。如果是以前,我會毫不猶豫寫幾行 C# 或 PowerShell 搞定,但在 2023 年練習用 AI 解決才是王道。試了 ChatGPT 跟 Bing Chat,調了幾版 Prompt,終於達成任務,花費時間比自己寫程式解析還久,但這不算選錯方法,而是我的吟唱技巧待加強:
(筆記:我的最終版 Prompt 為「請由以下文字取出 LenD1,LenD2, Mean,計算轉為CSV,只需要兩欄,第一欄位為 LenD1*100+LenD2*10,第二欄位取 Mean 不要 μs,資料間以","分隔」)
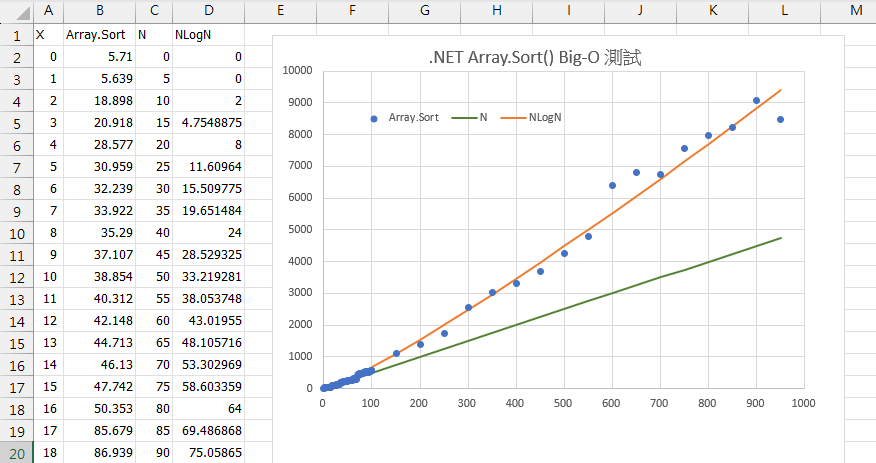
將資料貼入 Excel,順便練習繪成 X/Y 線圖,證明 Array.Sort() 執行時間大致吻合 N * Log(N, 2) 曲線!
心滿意足結束這回合綜合格鬥技演練。
Study of which sorting algorithm .NET Array.Sort() uses and benchmark test to observe its Big-O.
Comments
# by 佛弟子文獻學者孫守真任真甫
菩薩慈悲:末學也常是Bing大菩薩與chatGPT大菩薩混合著用,有時也請教YouChat大菩薩。感恩感恩 讚歎讚歎 南無阿彌陀佛 https://you.com/search?q=who+are+you&tbm=youchat&cfr=chat 現在則又有了 Bard大菩薩 (但目前只能用美語對話) https://bard.google.com/ 阿彌陀佛
# by Huang
吟唱技巧待加強....XD...和AI說話像在唸魔法咒語