Coding4Fun - 計算價差 Tick 數
 |  | 1 |  |  |
拿到一個有趣小題目,展開 C# 演算法自主練習。
有價證券有所謂的 Tick (檔位),意指申報價格的升降單位,通常會依價格高低區分級距,價格愈高,升降單位愈大。例如:未滿 10 元時升降單位為0.01元,10 元至未滿 50 元者為 0.05 元... 等。
某計算高低價格相差 Tick 數函式,採用很直覺的簡單寫法,從低價一個 Tick 一個 Tick 向上加直到等於高價,再統計經歷幾個 Tick。原本計算對象只差幾個 Tick,迴圈跑個三五次效能還 OK;但後來應用情境改變,可能出現相差數百上千個 Tick 的案例,數 Tick 的做法便顯得太沒效率。
來試試怎麼用 C# 改寫它。
假設 Tick 的級距設定如下:
| 價格 | Tick |
|---|---|
| Prz < 2 | 0.01 |
| 2 ≤ Prz < 5 | 0.02 |
| 5 ≤ Prz < 10 | 0.05 |
| 10 ≤ Prz < 25 | 0.10 |
| 25 ≤ Prz < 100 | 0.25 |
| 100 ≤ Prz < 200 | 0.50 |
| 200 ≤ Prz < 400 | 1 |
| 400 ≤ Prz | 2 |
先準備級距設定資料及測試用的題庫,題庫是以亂數產生 1000 筆高低價資料用來測試演算法,亂數種子固定,確保每次測試產生的題庫組合相同以求公平,而且不同演算法的計算結果可互相對答案,檢核有無算錯。
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
namespace TickCalcTest
{
/// <summary>
/// 級距資料
/// </summary>
public class Range
{
public int Index { get; private set; }
public decimal StartPrz { get; private set; }
public decimal EndPrz { get; private set; }
public decimal TickSize { get; private set; }
public int Qty { get; private set; }
public Range(int idx, decimal startPrz, decimal endPrz, decimal tickSize)
{
Index = idx;
StartPrz = startPrz;
EndPrz = endPrz;
TickSize = tickSize;
Qty = Convert.ToInt32((endPrz - startPrz) / tickSize + 1);
}
}
/// <summary>
/// 計算題
/// </summary>
public class Question
{
public decimal LowPrz { get; private set; }
public decimal HighPrz { get; private set; }
public int DiffTicks { get; set; }
public Question(decimal lowPrz, decimal highPrz)
{
LowPrz = lowPrz;
HighPrz = highPrz;
}
}
public class TestData
{
public static List<Range> TickSizes = new List<Range>()
{
new Range(0, 0, 1.99M, 0.01M),
new Range(1, 2, 4.98M, 0.02M),
new Range(2, 5, 9.95M, 0.05M),
new Range(3, 10, 24.9M, 0.10M),
new Range(4, 25, 99.75M, 0.25M),
new Range(5, 100, 199.5M, 0.5M),
new Range(6, 200, 399, 1),
new Range(7, 400, 5000, 2)
};
const int Seed = 8825252;
public static IEnumerable<Question> Questions
{
get
{
var rnd = new Random(Seed); //相同亂數種子產生相同題庫
return Enumerable.Range(0, 1000).Select(o =>
{
var rIdx = rnd.Next(TickSizes.Count);
var range = TickSizes[rIdx];
var prz1 = range.StartPrz + rnd.Next(range.Qty) * range.TickSize;
rIdx = rnd.Next(TickSizes.Count);
range = TickSizes[rIdx];
var prz2 = range.StartPrz + rnd.Next(range.Qty) * range.TickSize;
return new Question(Math.Min(prz1, prz2), Math.Max(prz1, prz2));
});
}
}
}
}
我打算寫三組演算法,第一組就是原始寫法 - while 迴圈累加 Tick 計數,第二組使用公式計算,第三組則預先將所有價格展開,直接查表。既然會有多組演算法,我將共用部分提取成抽象類別讓程式碼更簡潔。抽象類別 CalculatorBase.cs 如下:
using System;
using System.Collections.Generic;
using System.Linq;
namespace TickCalcTest
{
public abstract class CalculatorBase
{
protected readonly List<Range> TickSizeRanges;
protected Range GetTickSizeRange(decimal prz)
{
foreach (var ts in TickSizeRanges)
if (prz <= ts.EndPrz) return ts;
return TickSizeRanges.Last();
}
protected decimal GetTickSize(decimal prz) => GetTickSizeRange(prz).TickSize;
public Question[] Questions;
public CalculatorBase()
{
this.TickSizeRanges = TestData.TickSizes;
this.Questions = TestData.Questions.ToArray();
}
public abstract int CalcTicks(decimal lowPrz, decimal highPrz);
public void RunTest()
{
foreach (var q in Questions)
{
q.DiffTicks = CalcTicks(q.LowPrz, q.HighPrz);
}
}
public void OutputResult()
{
foreach(var q in Questions)
{
Console.WriteLine($"{q.LowPrz, 8:0.00} ~ {q.HighPrz, 8:0.00} => {q.DiffTicks, 8:n0} Ticks");
}
}
}
}
憨厚老實的一號選手出場,計算方式是從 lowPrz 開始,依當下價格級距不斷加上 Tick,直到等於 highPrz 為止,加幾次就是幾個 Tick,笨歸笨,但一定會有答案且不會出錯。
namespace TickCalcTest
{
public class DumbCalculator : CalculatorBase
{
public override int CalcTicks(decimal lowPrz, decimal highPrz)
{
var prz = lowPrz;
int count = 0;
while (prz < highPrz)
{
count++;
prz += GetTickSize(prz);
}
return count;
}
}
}
二號選手聰明一些,會找低價跟高價所在的級距,頭尾用與級距邊界價格差距除以 TickSize 計算,中間跳過部分則直接累加該級距總 Tick 數(這部分當然要用 LINQ 寫囉~);若高低價位在同一級距,則直接用二者價差除 TickSize 計算。
using System;
using System.Linq;
namespace TickCalcTest
{
public class FormulaCalculator : CalculatorBase
{
public override int CalcTicks(decimal lowPrz, decimal highPrz)
{
var loRange = GetTickSizeRange(lowPrz);
var hiRange = GetTickSizeRange(highPrz);
if (loRange.Index == hiRange.Index)
return Convert.ToInt32((highPrz - lowPrz) / loRange.TickSize);
return Convert.ToInt32((loRange.EndPrz - lowPrz) / loRange.TickSize) +
TickSizeRanges.Skip(loRange.Index + 1).TakeWhile(o => o.Index <= hiRange.Index - 1).Sum(o => o.Qty) +
Convert.ToInt32((highPrz - hiRange.StartPrz) / hiRange.TickSize) + 1;
}
}
}
三號選手則以空間換取時間,預先將 400 元以下所有可能出現的價格展開,計算各價位從 0 算起的 Tick 數存成 Dictionary。計算時,查表(400 元以上用算的)取得高低價的 Tick 數相減,瞬間得到 Ticks 數。
using System;
using System.Collections.Generic;
using System.Linq;
namespace TickCalcTest
{
public class LookUpCalculator : CalculatorBase
{
static decimal TopPrz = 0M;
static decimal TopTickSz = 0;
static int TopPrzTicks = 0;
static Dictionary<decimal, int> AllTicks = null;
static object syncObj = new object();
public LookUpCalculator() : base()
{
lock (syncObj)
{
if (AllTicks == null)
{
var prz = 0M;
TopPrz = TickSizeRanges.Last().StartPrz;
TopTickSz = TickSizeRanges.Last().TickSize;
AllTicks = new Dictionary<decimal, int>();
var count = 1;
while (prz < TopPrz)
{
AllTicks.Add(prz, count++);
prz += GetTickSize(prz);
}
TopPrzTicks = count;
}
}
}
int GetAbsTicks(decimal prz)
{
if (prz >= TopPrz)
return TopPrzTicks + Convert.ToInt32((prz - TopPrz) / TopTickSz);
return AllTicks[prz];
}
public override int CalcTicks(decimal lowPrz, decimal highPrz)
{
return GetAbsTicks(highPrz) - GetAbsTicks(lowPrz);
}
}
}
測試程式如下。我使用 BenchmarkDotNet 測量效能,實測前並用三種演算法各跑一次確認三種計算結果一致。
using BenchmarkDotNet.Attributes;
using BenchmarkDotNet.Running;
using System;
namespace TickCalcTest
{
class Program
{
static void Main(string[] args)
{
VerifyResult();
var summary = BenchmarkRunner.Run<TestRunner>();
}
private static void VerifyResult()
{
DumbCalculator dc = new DumbCalculator();
dc.RunTest();
FormulaCalculator fc = new FormulaCalculator();
fc.RunTest();
LookUpCalculator lc = new LookUpCalculator();
lc.RunTest();
bool pass = true;
for (var i = 0; i < dc.Questions.Length; i++)
{
if (dc.Questions[i].DiffTicks != fc.Questions[i].DiffTicks ||
dc.Questions[i].DiffTicks != lc.Questions[i].DiffTicks)
{
var q = dc.Questions[i];
Console.WriteLine(
$"{q.LowPrz,8:0.00} ~ {q.HighPrz,8:0.00} => {q.DiffTicks,8:n0} / {fc.Questions[i].DiffTicks,8:n0} / {lc.Questions[i].DiffTicks,8:n0}");
pass = false;
}
}
Console.WriteLine($"Verification Reustl = {(pass ? "PASS" : "FAIL")}");
if (!pass) throw new ApplicationException("Verification Failed");
}
}
public class TestRunner
{
[Benchmark]
public void RunDumbCalc()
{
var c = new DumbCalculator();
c.RunTest();
}
[Benchmark]
public void RunFormulaCalc()
{
var c = new FormulaCalculator();
c.RunTest();
}
[Benchmark]
public void RunLookupCalc()
{
var c = new LookUpCalculator();
c.RunTest();
}
}
}
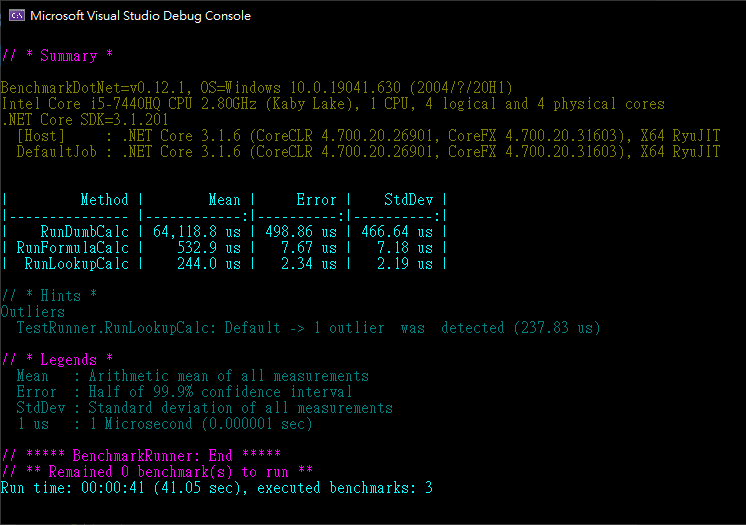
令人興奮的開獎時刻來臨,答案揭曉,愚公移山累加法平均耗時 64,119 μs,公式法快了 120 倍為 533 μs,查表法最快,時間再縮短一半以上,為 244 μs。
範例程式我已放上 Github,有興趣的同學可以拉回去玩。
Algorithm practice to calculate ticks between two stock prices with .NET.
Comments
# by CYHsu
謝謝大師,請收下我的膝蓋<(_ _)>